 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Однородные системы уравнений
|
|
Рассмотрим однородную систему линейных уравнений
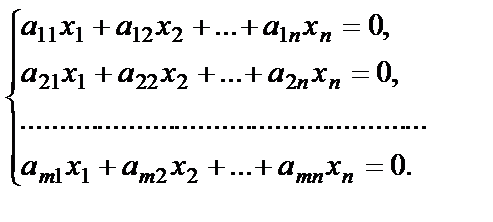 (26)
(26)
Однородная система всегда совместна (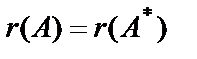 ), она имеет нулевое (тривиальное) решение
), она имеет нулевое (тривиальное) решение 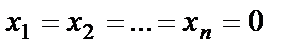 .
.
Для того, чтобы однородная система линейных уравнений имела ненулевые решения необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, то есть r<n.
Если число уравнений m системы совпадают с числом неизвестных n, то есть 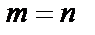 , основная матрица системы является квадратной, в этом случае условие r<n означает, что определитель основной матрицы системы
, основная матрица системы является квадратной, в этом случае условие r<n означает, что определитель основной матрицы системы 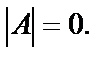
Пример 39. Решить систему уравнений
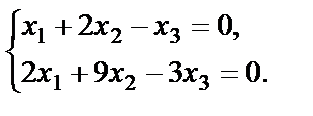
Решение. Составим основную матрицу системы
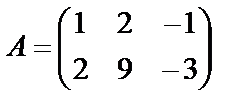 .
.
Элементы первой строки умножим на (-2) и прибавим к элементам второй строки.
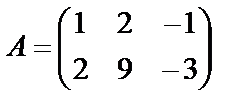 ~
~ 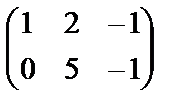 .
.
Получили матрицу ступенчатого вида, в которой две ненулевые строки, поэтому ранг матрицы 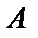 , а значит и расширенной матрицы
, а значит и расширенной матрицы  равен 2, то есть
равен 2, то есть 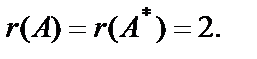
Число неизвестных в системе уравнений равно 3, r<n, поэтому данная система имеет ненулевые решения.
Для составления системы, равносильной данной, воспользуемся преобразованной матрицей

Из второго уравнения выразим 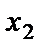 через
через 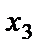 , при этом
, при этом 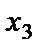 будет является свободной переменной:
будет является свободной переменной:  .
.
Полученную правую часть равенства подставим в первое уравнение и выразим 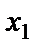 через
через 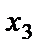 :
: 
Пусть 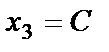 , тогда общее решение системы можно записать в виде матрицы-столбца
, тогда общее решение системы можно записать в виде матрицы-столбца
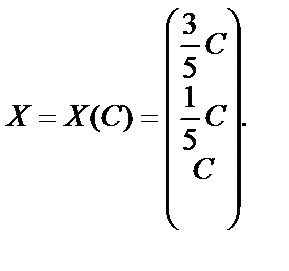 (27)
(27)
Пример 40. Решить систему уравнений
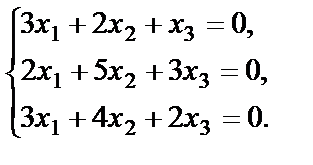
Решение. Выпишем основную матрицу системы
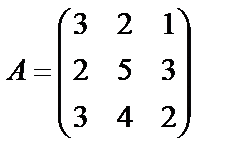 .
.
Элементы первой строки умножим на (-2) и прибавим к соответствующим элементам второй строки умноженным на 3:
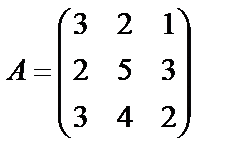 ~
~ 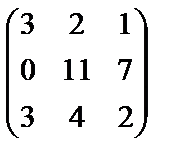 .
.
Элементы первой строки умножим на (-1) и прибавим к элементам третьей строки
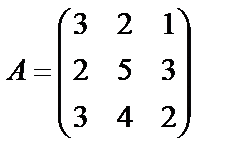 ~
~ 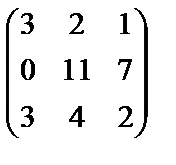 ~
~ 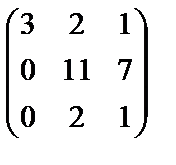 .
.
Элементы второй строки умножим на (-2), элементы третьей строки на 11 и полученные строки сложим
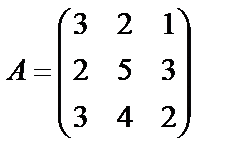 ~
~ 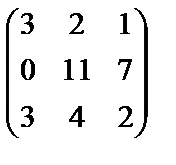 ~
~ 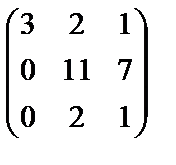 ~
~ 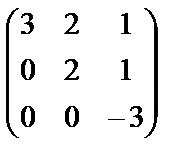 .
.
Получили три ненулевые строки, значит ранг матрицы 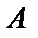 равен 3, число неизвестных в системе уравнений тоже равно 3, то есть
равен 3, число неизвестных в системе уравнений тоже равно 3, то есть 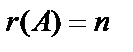 , значит данная система уравнений имеет единственное решение – нулевое, то есть
, значит данная система уравнений имеет единственное решение – нулевое, то есть
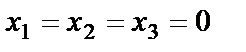 .
.
Пример 41. Решить систему уравнений

Решение. Выпишем основную матрицу системы
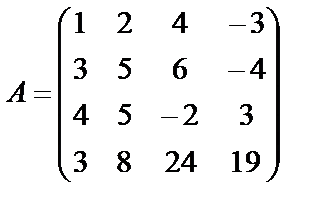
и найдем ранг этой матрицы.
Элементы первой строки умножим на (-3) и прибавим к элементам второй и четвертой строк, затем элементы первой строки умножим на
(-4) и прибавим к третьей строке:
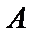 ~
~ 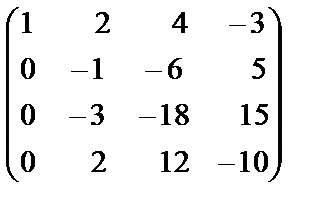 .
.
Элементы второй строки умножим на 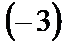 и прибавим к элементам третьей строки, затем элементы второй строки умножим на
и прибавим к элементам третьей строки, затем элементы второй строки умножим на 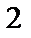 и прибавим к элементам четвертой строки:
и прибавим к элементам четвертой строки:
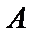 ~
~ 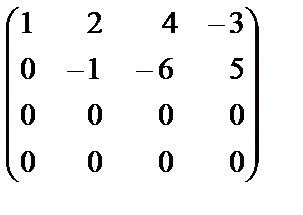 .
.
В преобразованной матрице ступенчатого вида получилось две ненулевые строки, поэтому ранг матрицы 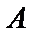 равен двум, то есть
равен двум, то есть 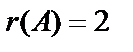 , а число неизвестных в системе уравнений равно 4 (
, а число неизвестных в системе уравнений равно 4 ( ). Получили, что
). Получили, что  , поэтому данная система уравнений имеет ненулевые решения. Укороченная система имеет вид:
, поэтому данная система уравнений имеет ненулевые решения. Укороченная система имеет вид:
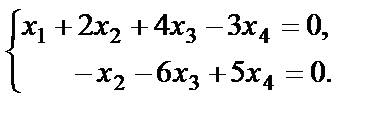
Выразим 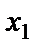 и
и 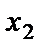 через
через 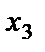 и
и  :
: 
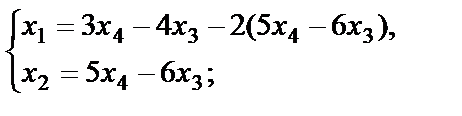 или
или 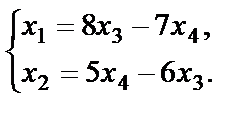
Неизвестные 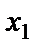 и
и 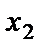 - базисные, а
- базисные, а 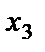 и
и  - свободные. Полагая
- свободные. Полагая 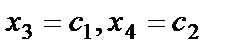 , получим общее решение системы, записанное в виде матрицы-столбца (1.27)
, получим общее решение системы, записанное в виде матрицы-столбца (1.27)
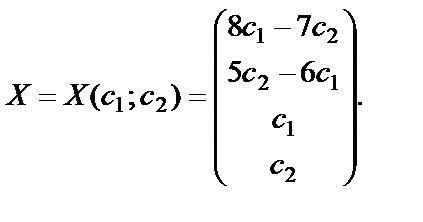 (28)
(28)
Назовем фундаментальной системой решений систему матриц-столбцов, полученную из общего решения при условии, что свободным неизвестным дают последовательно значения
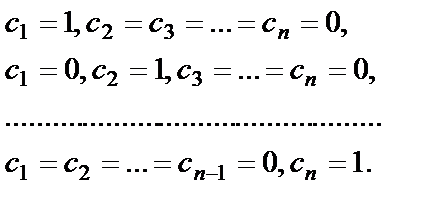
Матрицы-столбцы, то есть фундаментальную систему решений обозначают  . Общее решение будет представлено в виде
. Общее решение будет представлено в виде
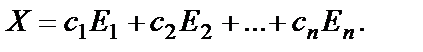 (29)
(29)
В примере 41 найдем фундаментальную систему решений и выразим с ее помощью общее решение этой системы.
Из общего решения (28) системы найдем 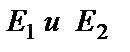 :
:
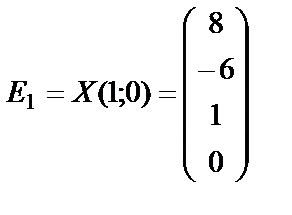 ,
, 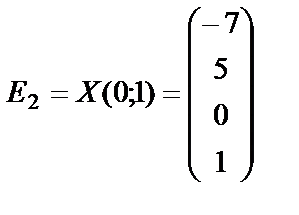 . (30)
. (30)
С использованием фундаментальной системы (30) общее решение (28) может быть записано в виде (29)
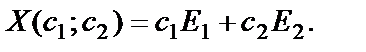
Дата публикования: 2015-10-09; Прочитано: 345 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
