 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определители третьего порядка
|
|
Определение. Определителем третьего порядка, соответствующим квадратной таблице элементов
 ,
,
называется число, определяемое равенством
 (2)
(2)
Пример 4. Вычислить определитель
 .
.
Решение. По определению получим: 
Если в формуле (2) раскрыть определители второго порядка и собрать слагаемые с одинаковыми знаками, то получим:
 (3)
(3)
Этот способ вычисления определителя третьего порядка называется правилом треугольника.
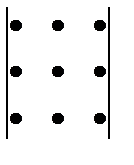

Первые три слагаемых для вычисления определителя есть сумма произведений элементов главной диагонали и элементов, расположенных в вершинах треугольников, как они показаны линиями на первом рисунке; оставшиеся слагаемые есть сумма произведений, взятых со знаком минус, элементов побочной диагонали и элементов, расположенных в вершинах треугольников, как они показаны линиями на втором рисунке.
Пример 5. Вычислить определитель  по правилу треугольника.
по правилу треугольника.
Решение. Перемножим элементы главной диагонали определителя 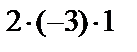 , затем – элементы, лежащие на параллелях к этой диагонали, и элементы из противоположного угла определителя согласно правилу треугольника
, затем – элементы, лежащие на параллелях к этой диагонали, и элементы из противоположного угла определителя согласно правилу треугольника  ,
,  . Элементы, входящие в формулу (3) со знаком минус, вычисляем аналогично, но относительно побочной диагонали:
. Элементы, входящие в формулу (3) со знаком минус, вычисляем аналогично, но относительно побочной диагонали: 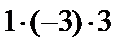 ,
,  ,
,  .
.
Таким образом 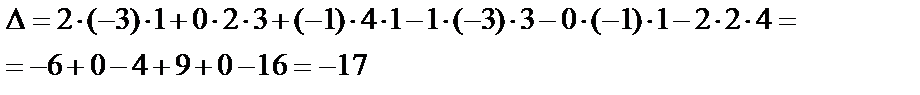
Определение. Определитель, в котором под главной диагональю (над главной диагональю) стоят нули, называется определителем треугольного вида.
Определитель треугольного вида равен произведению элементов главной диагонали.
Пример 6. Вычислить определитель  .
.
Решение. По условию дан определитель треугольного вида, т.к. под главной диагональю этого определителя стоят нули, значит значение данного определителя равно произведению элементов главной диагонали, то есть  .
.
Определение. Минором элемента определителя третьего порядка называется определитель второго порядка, полученный из данного определителя путем вычеркивания строки и столба, на пересечении которых стоит данный элемент.
Минор элемента  , стоящего на пересечении i -ой строки и j -го столбца определителя, обозначают
, стоящего на пересечении i -ой строки и j -го столбца определителя, обозначают  .
.
Например, для определителя

миноры  ,
,  .
.
Определение. Алгебраическим дополнением данного элемента определителя 3-го порядка называется минор этого элемента, умноженный на  , где k равно сумме номера строки и номера столбца, на пересечении которых находится этот элемент.
, где k равно сумме номера строки и номера столбца, на пересечении которых находится этот элемент.
Алгебраическое дополнение элемента  обозначают
обозначают  . Согласно определению
. Согласно определению  .
.
Для определителя третьего порядка знак, который при этом приписывается минору соответствующего определителя, определяется следующей таблицей:  .
.
Из определения определителя третьего порядка следует, что
 .
.
Верна общая теорема разложения: определитель третьего порядка равен сумме произведений элементов любой его строки или столбца на соответствующие этим элементам алгебраические дополнения.
Таким образом, имеют место шесть разложений:
 (5)
(5)
Отметим, что сумма произведений элементов какого-либо ряда (строки или столбца) на алгебраические дополнения элементов параллельного ряда равна нулю.
Пример 7. Вычислить определитель 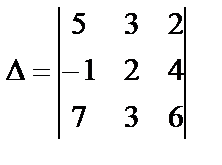 ,
,
разлагая его по элементам третьего столбца.
Решение. Согласно теореме разложения имеем:

Дата публикования: 2015-10-09; Прочитано: 1084 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
