Основные классические теоремы о замечательных точках косого четырехугольника

Теорема Лейбница. Сумма квадратов расстояний произвольной точки Р до вершин косого четырехугольника (тетраэдра) А₁А₂А₃А₄ равна сумме квадратов расстояний его центроида G до вершин, сложенной с учетверенным квадратом расстояния точки Р до центроида G (рис. 1.4).

. (1.8)

Рисунок 1.4

Доказательство:

Пусть А₁А₂А₃А₄- косой четырехугольник, G- его центроид и Р- произвольная точка (рис.1.4). Рассмотрим треугольники A₁PG, A₂PG, A₃PG, A₄PG. Учитывая, что

, , ,

и

, ,

, ,

получим:

Но , что непосредственно следует из (1.1) при условии, если полюс помещен в точку G. Следовательно, равенство (1.8) доказано.

Теорема Менелая. Пусть на прямых А₁А₂, А₂А₃, А₃А₄, А₄А₃ определяющих косой четырехугольник А₁А₂А₃А₄ даны соответственно точки P₁₂,Р₂₃,Р₃₄,Р₄₁. Для того чтобы эти точки лежали в одной плоскости, необходимо и достаточно, чтобы:

. (1.9)

Доказательство:

Для доказательства указанные отношения обозначим:

, , ,

Тогда необходимо доказать, что l₁l₂l₃l₄=1.

,

.

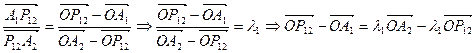Аналогично для l₂,l_3,,l₄. тогда:

. (1.10)

(i=1,2,3,4; j=i+1, если i=1,2,3, и j=1,если i=4).

Из (1.2)

Следовательно матрица нормированных барицентрических координат точек P_ij относительно тетраэдра А₁А₂А₃А₄ будет иметь вид:

При помощи элементарных преобразований строк матрица может быть приведена к

Так как элементарные преобразования не изменяют ранга матрицы, то ранги матриц и одинаковы. Очевидно, ранг матрицы не ниже трех. Для того, что бы он был равен трем, необходимо и достаточно, что бы =1. При этом и только при этом условии точки P_ij будут лежать в одной плоскости.

Теорема Чевы.. Пусть на прямых A₁A₂, А₂А₃, А₃А₄, А₄А₁, определяющих косой четырехугольник А₁А₂А₃А₄, даны точки Р₁₂,Р₂₃,Р₃₄, Р₄₁. Для того, чтобы плоскости Р₁₂А₃А₄, Р₂₃А₄А₁, Р₃₄А₁А₂, Р₄₁А₂А₃ пересекались в одной точке Р, необходимо и достаточно, чтобы

(1.11)

Рисунок 1.5

Доказательство:

Необходимость. Пусть А₁А₂А₃А₄- косой четырехугольник, прямые РА₁, РА₂,РА₃,РА₄ пересекают плоскости А₂А₃А₄, А₃А₄А₁, А₄А₁А₂, А₁А₂А₃ в точках Р₁,Р₂,Р₃,Р₄ (рис. 1.5). По теореме Чевы1) для треугольника А₁А₂А₃ и точки Р₄ имеем

.

­­­­­­­­­По той же теореме для треугольника А₃А₄А₁ и точки Р₂:

.