Косой четырехугольник. Элементы косого четырехугольника и их свойства

Пространственным невырожденным или косым четырехугольником будем называть четырехугольник, вершины которого не принадлежат одной плоскости.

Четырехугольник, все вершины которого принадлежат одной плоскости, будем называть вырожденным косым четырехугольником.

Если A₁A₂A₃A₄ – косой четырехугольник (рис. 1.1), то отрезки А₁А₂, А₂А₃, А₃А₄, А₄А₁ называют его сторонами, а плоскости, определяемые каждыми тремя вершинами, его гранями.

Теорема. Отрезки, соединяющие середины противоположных сторон и середины диагоналей косого четырехугольника, пересекаются в одной точке и делятся в ней пополам

Рисунок 1.1

Доказательство:

Пусть A₁A₂A₃A₄ – косой четырехугольник, М, Е, F, N – середины его сторон, точка О - произвольная точка пространства (рис 1.1). Тогда

, ,

, .

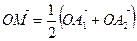
Пусть G₁, G₂-середины МЕ, FN соответственно. Тогда

,

.

Отсюда следует .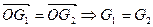

Пусть G₃ –середина диагонали LQ. Учитывая, что

, , ,

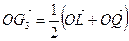
получаем

.

Видно что

,

Отсюда следует

,

то есть

. (1.1)

Точку G будем называть центроидом косого четырехугольника.

Все рассуждения останутся верными, если косой четырехугольник вырождается в плоский.

Теорема. Сумма квадратов расстояний от точки до вершин косого четырехугольника (тетраэдра) наименьшая для его центроида.

Рисунок 1.2

Доказательство:

Пусть A₁A₂A₃A₄ – косой четырехугольник. Введем прямоугольную декартову систему координат, как указано на рисунке 1.2. Тогда

A₁(х₁,0,0), A₂(х₂,y₂,0), A₃(х₃,y₃,0), A₄(0,0,z₄).

Точка Р(х,y,z) - произвольная точка пространства.

Составим функцию для трех переменных:

.

Найдем ее минимум. Для этого решим систему:

.

.

Точка Р имеет координаты (, , ). Легко показать, что в точке Р функция имеет min.

Теперь найдем координаты центроида при таком расположении системы координат:

.

Получили,что P=G, что и доказывает теорему.

Медианами косого четырехугольника будем называть отрезки, соединяющие его вершины с центрами треугольников противоположных граней.

Теорема (о пересечении “медиан”). Медианы косого четырехугольника пересекаются в его центроиде и делятся в нем в отношении 3:1, считая от вершины.

Рисунок 1.3

Доказательство:

Пусть A₁A₂A₃A₄ – косой четырехугольник, G, A₁G₁, А₂G₂, А₃G₃, A₄G₄ -его центроид и медианы соответственно (рис 1.3).

Из (1.1)

.

Из треугольников А₂А₃А₄, А₁GO, А₁G₁O

, , .

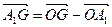Тогда получаем

То есть точка G делит в отношении 3:1, считая от вершины.

Аналогично доказывается для , , . Таким образом медианы косого четырехугольника пересекаются в его центроиде и делятся в нем в отношении 3:1, считая от вершины.

1.2 Барицентрические координаты точек пространства

Если полюс выбрать вне трехмерного пространства четырехугольника А₁А₂А₃А₄, то радиус-вектор любой точки Р этого пространства через радиус-векторы вершин данного косого четырехугольника выражается так

. (1.2)

В самом деле, векторы линейно независимы и поэтому по ним однозначным образом разлагается вектор . Однако четыре вектора 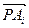в трехмерном пространстве всегда линейно зависимы и поэтому:

. (1.3)

причем не все равны нулю одновременно. Но:

, , , .

Следовательно, пользуясь равенством (1.2), получаем:

,

,

,

.

Если эти четыре вектора (i =1,2,3,4) подставить в (1.3.), то получим уравнение

относительно (к =1,2,3,4),которое может быть удовлетворено лишь тогда, когда все коэффициенты при равны 0, либо векторы линейно независимы. Это приводит к системе четырех линейных однородных уравнений относительно . Собираем коэффициенты при :

.

Так как линейно независимы, то коэффициенты при них должны равняться 0. Приходим к системе уравнений

Данная система относительно (i =1,2,3,4) имеет ненулевое решение, если ее определитель равен 0, то есть

.

Раскрывая определитель, получаем

,

.

Итак, каждой точке Р пространства четырехугольника А₁А₂А₃А₄ соответствуют четыре числа a₁,a₂,a₃,a₄, сумма которых равна 1. Эти числа называются нормированными барицентрическими координатами точки Р относительно косого четырехугольника А₁А₂А₃А₄ .

Покажем, что числа a_i не зависят от выбора полюса О. Для этого возьмем другую точку О₁ и, докажем, что:

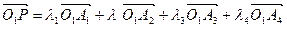, (1.4)

где l_i - барицентрические координаты точки Р, определенные выше с помощью косого четырехугольника А₁А₂А₃А₄ и точки О, то есть

Действительно:

поэтому

.

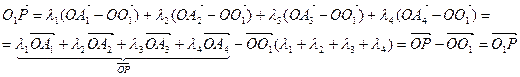Таким образом, независимость барицентрических координат l_i от выбора точки доказана.

Аффинный и метрический смысл барицентрических координат в пространстве

С геометрической точки зрения нормированные барицентрические координаты l_i точки Р равны отношениям объемов двух ориентированных тетраэдров: объема тетраэдра, полученного путем замены соответствующей вершины тетраэдра А₁А₂А₃А₄ точкой Р, к объему тетраэдра А₁А₂А₃А₄:

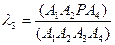, , , . (1.5)

Пусть d_i – ориентированные расстояния точки Р до граней данного тетраэдра, причем за положительное направление принято направление соответствующей высоты h_i тетраэдра А₁А₂А₃А₄ от вершины к противоположной грани. Тогда отношения объемов указанных тетраэдров, очевидно равны (i=1,2,3,4), таким образом,

, (1.6)

а значит,

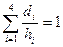. (1.7)