 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Производная по направлению. Градиент
|
|
Пусть функция 
дифференцируема в области 
и пусть в этой области задано некоторое направление 
. Производная функции по направлению 
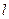находится по формуле
(1)
Если производные 
вычислены в фиксированной точке 
, то формула (1) показывает скорость изменения функции в этой точке по направлению 
. Выясним, по какому направлению функция в данной точке возрастает быстрее.
Введем вектор с координатами 
. Такой вектор называется градиентом функции и обозначается символом 
:
(2)
Левая часть формулы (1) теперь может рассматриваться как скалярное произведение единичного вектора на вектор . Значит, можем записать
,
где 
– угол между направлением и градиентом. Отсюда видно, что производная 
достигает наибольшего значения, когда 
, т.е. когда направление совпадает с градиентом.
Таким образом, скорость наибольшего роста функции в данной точке (по величине и направлению) определяется градиентом функции.
Пример 1. Найти производную функции 
в точке 
в направлении 
. Чему равна величина градиента функции в этой точке?
Решение. Чтобы воспользоваться формулой (1), подсчитаем частные производные заданной функции в точке 
:
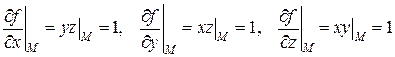
Значит, производная функции в заданном направлении равна
.
В соответствии с формулой (2) запишем градиент функции в точке :
Величина градиента (модуль вектора) равна 
. ☻
Пример 2. Найти производную функции 
в точке 
в направлении, составляющем угол 
с положительным направлением оси 
.
Решение. Подсчитаем сначала частные производные в точке :
.
Найдем направляющие косинусы:
.
По формуле (1) запишем
. ☻
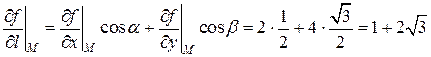Пример 3. Для функции 
определить угол между градиентами в точках 
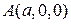и 
.
Решение. Подсчитаем сначала частные производные функции в точках 
:
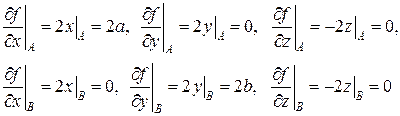
Теперь можем записать градиент функции в каждой из этих точек:
,
.
Скалярное произведение этих векторов равно нулю:
.
Значит, угол между градиентами равен 
. ☻
Дата публикования: 2015-10-09; Прочитано: 870 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
