Дифференцирование неявных функций

Уравнение

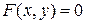(1)

связывает координаты точек на плоскости, задавая тем самым неявную функцию . Найти эту функцию явно из уравнения (1), вообще говоря, нельзя. Но производную 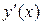неявной функции можно определить, продифференцировав тождество по переменной .

Пример 1.. Найти производную функции , заданной неявно уравнением

.

Решение. Пусть – функция, определяемая неявно заданным уравнением, то есть имеет место тождество .

Продифференцируем это тождество по переменной :

.

Отсюда находим производную :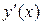

. ☻

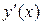Если частные производные функции существуют и , то производная неявной функции определяется из соотношения

.

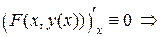
Получаем формулу

. (2).

Пример 1а. Найдём другим методом производную функции , заданной неявно уравнением (пример 1).

Решение. Подсчитаем частные производные

,

По формуле (2) получаем производную неявной функции :

(при условии ). ☻

Пример 2. Найти 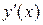и функции , заданной неявно уравнением

.

Решение. Подсчитаем частные производные функции :

,

.

В соответствии с формулой (2) запишем , . Продолжаем дифференцировать по переменной , не забывая, что :

.

Остается подставить уже найденную производную :

, . ☻

Уравнение связывает координаты точек в трехмерном пространстве и задает неявную функцию . Как и выше, не всегда можно найти саму функцию , но можно найти ее частные производные 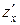, , продифференцировав тождество по переменным и :

.

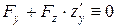Из полученных соотношений находим

, , (3)

Естественно, при этом предполагается, что частные производные функции существуют и .

Пример 3. Найти частные производные первого и второго порядков функции , заданной неявно соотношением .

Решение. Подсчитаем частные производные функции :

, , .

В соответствии с формулами (3) запишем

, ,

Продолжая дифференцировать, получим (с учетом найденных , ):

.

Естественно, полагаем . ☻

Пример 4. Найти частные производные функции , заданной уравнением

.

Решение. Можно не пользоваться готовыми формулами (3), а (см. пример 1) подставить предполагаемое решение уравнения – функцию в заданное соотношение и затем дифференцировать полученное тождество.

Дифференцируем тождество по :

Дифференцируем по :

Оба равенства корректны, если . ☻

Рассмотрим случай, когда функции заданы неявно системой уравнений

(4)

Функции и их частные производные мы предполагаем непрерывными в некоторой области. Кроме того, предполагаем, что якобиан

Покажем, как получить частные производные неявных функций .

Пусть – именно те функции, которые определены системой (4). Подставляя эти функции в уравнения (4), получим тождества

.(5)

Дифференцируя эти тождества по переменной , получим систему линейных уравнений относительно неизвестных :

(6)

Продифференцируем тождества (5) по переменной :

(7)

Получили систему линейных уравнений относительно неизвестных .

По условию, определитель систем (6) и (7) . В силу теоремы Крамера каждая из этих систем имеет единственное решение.

Пример 5. Найти частные производные функций , заданных неявно системой уравнений

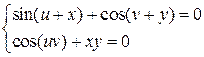
Решение. Записываем тождества

. (8)

Дифференцируем каждое тождество (8) по переменной :

Вычислим определитель системы (якобиан ):

.

Предполагаем, что .

Далее вычисляем

Остается по формулам Крамера найти

.

Теперь дифференцируем каждое тождество (8) по переменной :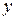

Находим

Наконец, находим

. ☻

Если функции 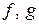дважды дифференцируемы, то можно находить вторые производные неявных функций , дифференцируя тождества (6) и (7).

Пример 6. Найти первые и вторые производные функций , заданных неявно системой уравнений .

Решение. Записываем тождества

. (*)

Дифференцируем каждое их них сначала по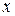

Полученную систему относительно неизвестных 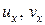можно упростить с помощью первого из заданных уравнений, откуда . Тогда

(9)

Дифференцируем тождества (*) по :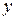

Второе из заданных уравнений дает , что позволяет записать систему относительно неизвестных 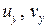в виде:

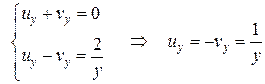(10)

Продолжая дифференцировать, находим

. ☻

Умение вычислять производные неявно заданных функций пригодится при изучении темы «Замена переменных».