 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Система аксиом Вейля
|
|
В 1917 – 1918 годах известный немецкий математик Герман Вейль (1885 – 1955) предложил векторное обоснование геометрии Евклида. В этой системе за исходные объекты взяты «вектор» и «точка», за основные отношения – «сумма векторов», «умножение вектора на число», «скалярное произведение», «отложение вектора от точки». Система векторов для трехмерного пространства состоит из 17 аксиом, разбитых на пять групп:
1.Аксиомы сложения векторов (4).
2.Аксиомы умножения вектора на число (4).
3.Аксиомы скалярного произведения (5).
4.Аксиомы размерности (2).
5.Аксиомы отложения вектора (2).
I группа. Аксиомы сложения векторов
Основное отношение: каждым двум векторам 
и 
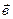соответствует один определенный вектор 
, который называется их суммой и обозначается 
.
1.1. Для каких-либо двух векторов 
и 
.
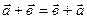1.2. Для каких-либо трех векторов 
1.3. Существует такой вектор 
, что 
для любого вектора .
Вектор называется нулевым вектором.
1.4. Для любого вектора найдется вектор 
, что 
. Вектор называется противоположным вектором для вектора , и обозначается 
.
II группа. Аксиомы умножения вектора на число
Основные отношения: каждому вектору и каждому действительному числу k соответствует один определенный вектор, который называется произведением вектора на число k и обозначается 
.
2.1. 
для любого вектора .
2.2. 
для любого вектора и любых действительных чисел 
2.3. 
для любого вектора и любых действительных чисел
2.4. 
для любых векторов 
и любого действительного числа k.
III группа. Аксиомы скалярного произведения векторов (метричные аксиомы)
Основные отношения: каждым двум векторам и соответствует одно определенное действительное число, которое называется скалярным произведением и обозначается 
.
3.1.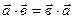 
для любых двух векторов и .
3.2. 
для любых векторов 
3.3. 
для любых векторов и любого действительного числа 
3.4. 
для произвольного вектора .
3.5. 
тогда и только тогда, если 
.
IV группа. Аксиомы отложения вектора
Основные отношения: каждой паре точек А, В соответствует один определенный вектор, который обозначается 
5.1. Для любой точки А и какого-либо вектора существует единственная точка В, что 
(в таком случае говорят, что точку В получили путем отложения вектора от точки А).
5.2.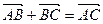 
для любых трех точек А, В и С.
Дата публикования: 2015-10-09; Прочитано: 1204 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
