III. Аксиомы конгруэнтности

Эта группа аксиом определяет понятие конгруэнтности для отрезков и углов

. Если А и В – разные точки на прямой а и - точка на этой же прямой или на другой , то всегда можно найти точку , которая лежит в данную сторону от точки А прямой , причем такую, что отрезок АВ конгруэнтен отрезку . Обозначают 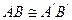(рис.9).

. Если два отрезка конгруэнтны третьему, тони между собой конгруэнтны, то есть, если .

. Пусть АВ и ВС – два отрезка прямой а, которые не имеют общих точек, и пусть - два отрезка этой же прямой или прямой , которые тоже не имеют общих точек. Если, при этом , то и (рис. 10).

. От данной прямой в данную полуплоскость, которая определяется данной полупрямой и ее продолжением, можно отложить угол, и причем единственный, конгруэнтный данному углу (рис.11).

. Если в двух треугольниках АВС и и , то у них (рис. 12).