 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод Фурье для конечного стержня
|
|
Уравнение теплопроводности относится к уравнениям параболического типа.
Будем искать решение уравнения теплопроводности с начальными и граничными условиями:

Частные решения данного уравнения будем искать в виде:
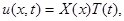
где X (x) – функция только переменного x; T (t) – функция только переменного t.
Подставляя предполагаемую форму решения в уравнение, получим:
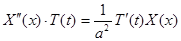
или, после деления на 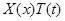 ,
,
 .
.
Правая часть этого равенства является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение
 ,
,
где 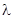 – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций
– постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций 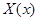 и
и  :
:
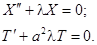
Очевидно, что нас интересуют нетривиальные решения (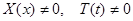 ).
).
Граничные условия дают:
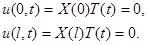
Отсюда следует
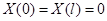 .
.
Таким образом, мы приходим к простейшей задаче: найти те значения параметра 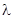 , при которых существуют нетривиальные решения задач
, при которых существуют нетривиальные решения задач

а также найти эти решения.
При решении уравнения колебания струны было доказано, что при 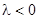 и
и  уравнение
уравнение  имеет только тривиальные решения, поэтому рассмотрим только случай
имеет только тривиальные решения, поэтому рассмотрим только случай 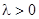 . Тогда решение уравнения
. Тогда решение уравнения  с учетом граничных условий
с учетом граничных условий  имеет вид
имеет вид
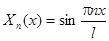 ,
,
а решение уравнения 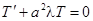 имеет вид
имеет вид
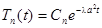 ,
,
где  – неопределенный пока коэффициент.
– неопределенный пока коэффициент.
Тогда частные решения уравнения теплопроводности
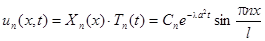 ,
,
а общее решение
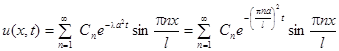 .
.
Начальные условия позволяют определить  :
:
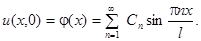
Для выполнения этого начального условия необходимо взять в качестве  коэффициент Фурье:
коэффициент Фурье:

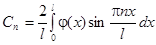 .
.
Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.
Пример. Найти решение уравнения теплопроводности при граничных условиях 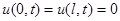 и начальном условии
и начальном условии 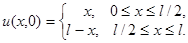
Решение. Общее решение уравнения имеет вид
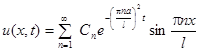 ,
,
где  .
.
Вычисляя данные интегралы, получим:
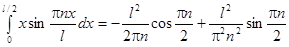 ;
; 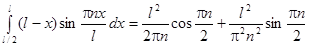 .
.
Итак, 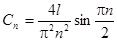 . Так как
. Так как 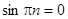 , то
, то  .
.
Решение имеет вид
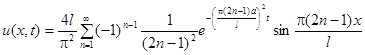 .
.
Дата публикования: 2015-10-09; Прочитано: 534 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
