Уравнение Лапласа в прямоугольнике

Для решения уравнения Лапласа в прямоугольнике необходимо рассмотреть вспомогательную задачу.

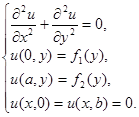
Решим эту задачу методом разделения переменных. Будем искать решение в виде

.

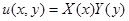Уравнение примет вид

.

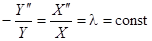Отсюда получим два обыкновенных дифференциальных уравнения

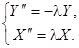
Определим знак .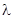

1. Пусть 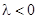, например .
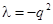Рассмотрим уравнение

.

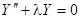Характеристическое уравнение имеет вид

Получаем 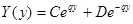– решение первого уравнения системы.

Рассмотрим уравнение

.

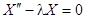Характеристическое уравнение имеет вид

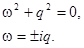
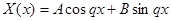– решение второго уравнения системы.

Таким образом,

.

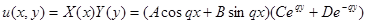Удовлетворим краевым условиям:

,

.

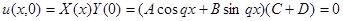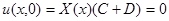, так как мы ищем ненулевые решения уравнения, тогда 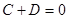, отсюда .

.

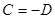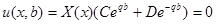Учитывая, что 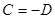имеем

.

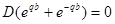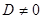, следовательно, 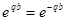. Это возможно только при 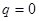, но тогда мы получим решение уравнения, равное постоянной, а это не удовлетворяет краевым условиям задачи.

2. Пусть 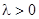, например .
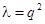Тогда решения системы уравнений имеют соответственно вид

;

.

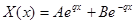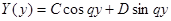Таким образом,

.

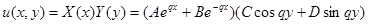Удовлетворим краевым условиям:

.

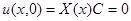, следовательно, .

.

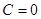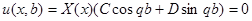Помня, что 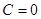, имеем:

.

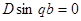Так как при 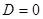получим нулевое решение, то

.

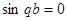Отсюда

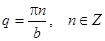
Итак, получили решение

.

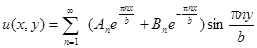Подставим начальные условия:

.

Отсюда

;

.

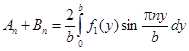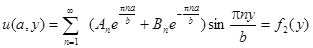Отсюда

.

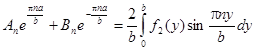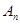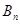Для нахождения коэффициентов и необходимо решить систему уравнений:

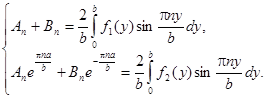
Подставив полученные коэффициенты, получим решение задачи.

Рассмотрим ненулевые краевые условия для уравнения Лапласа в прямоугольнике:

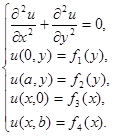
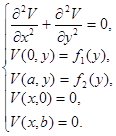Решение задачи будем искать в виде суммы двух функций . Иными словами необходимо решить две системы уравнений:

и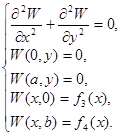

Первая система уже решена. Для того, чтобы найти решение второй системы, необходимо просто заменить соответствующие буквы и цифры в решении для 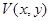, т.е. .