 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свободное закрепление
|
|
Теперь рассмотрим случай, когда при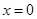 
мы имеем свободный конец. Это значит, что касательная в точке 0 параллельна оси x:
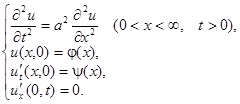
Делаем четное продолжение функций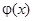 
и 
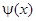. Получим решение уравнения колебаний в виде функции
,
определенной для всех 
. В силу леммы 2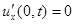 
.
Кроме того, эта функция удовлетворяет пр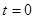и 
и 
следующим начальным условиям:
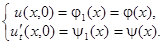
Таким образом, рассматривая полученную функцию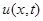 
только для 
, мы получим функцию, удовлетворяющую всем условиям поставленной задачи.
Вывод. Для решения задачи на полуограниченной прямой с граничным условием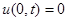 
начальные данные надо продолжить на всю прямую нечетным образом.
Для решения задачи на полуограниченной прямой с граничным условием 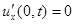начальные данные надо продолжить на всю прямую четным образом.
2.2.4. Метод продолжения для конечной струны (начальная и конечная точки жёстко закреплены)
Рассмотрим краевую задачу для ограниченного отрезка (0, l). Будем искать решение уравнения
,
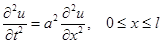удовлетворяющее граничным условиям
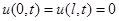
и начальным условиям
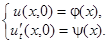
Будем искать решение задачи методом продолжения, предполагая возможность следующего представления:
,
где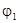 
(x) и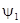 
(x) – функции, подлежащие определению. Начальные условия
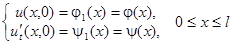
определяют значения 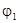(x) и 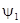(x) в интервале (0, l).
Для того чтобы удовлетворить нулевым граничным условиям, наложим на функци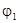и (x) и 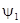(x) требования нечетности относительно точек x = 0, x = l:
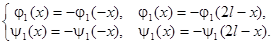
Сопоставляя эти равенства, получим:
и аналогично для Ψ(x), т.е. 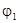(x) и 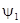(x) – периодические функции с периодом 2 l.
Нетрудно видеть, что условия нечетности относительно начала координат и условия периодичности определяют продолжение 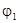(x) и 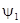(x) на всей прямой 
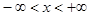. Подставляя их, получаем решение задачи.
Пример. Решить уравнение колебания полубесконечной струны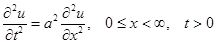 
, удовлетворяющее условиям:
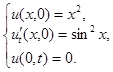
Решение. Имеем задачу свободных колебаний полубесконечной струны (с краевым условием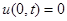 
). Так как 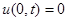, то продолжим функци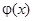и и 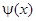на отрицательную полуось нечетным образом
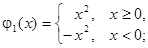
Тогда по формуле Даламбера:
=
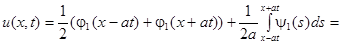
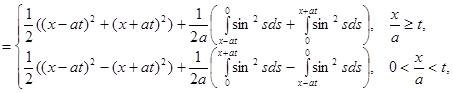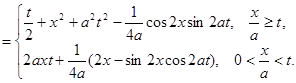
Пример. Решить уравнение колебания полубесконечной струны 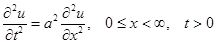, удовлетворяющее условиям:
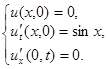
Решение. Имеем задачу свободных колебаний полубесконечной струны (с краевым условием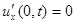 
). Так как 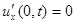, то продолжим функцию 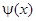на отрицательную полуось четным образом (
):
, 
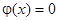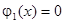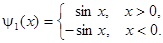
Тогда по формуле Даламбера:
= 
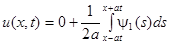
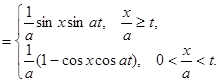
Дата публикования: 2015-10-09; Прочитано: 1171 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
