Использование метода сеток для решения гиперболических уравнений

Решение гиперболических уравнений также можно осуществить с помощью разностных схем. Разностные схемы решения одномерного гиперболического уравнения рассмотрим на примере следующего уравнения:

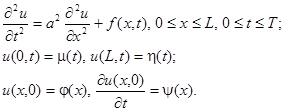
Построим сетку 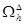, в которой будем искать решение уравнения. Производную 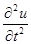заменим соотношением:

,

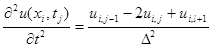остальные производные такие же, как и в предыдущем подразделе.

Получим следующую явную разностную схему решения уравнения:

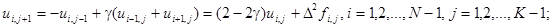
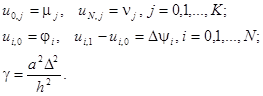
Она устойчива при 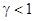и по аналогии с разностной схемой (см.подраздел 1.4.1.) может быть легко запрограммирована в MATLAB.

В качестве примера рассмотрим следующую задачу.

Пример. Решить начально-граничную задачу:

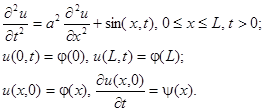
Ниже представлена функция giperbol решения данного уравнения, а на рис.1.4 – график полученного решения. Параметры функции аналогичны рассмотренным ранее, т.е. в подпрограмме решения параболического уравнения.

function [u,x,t]=giperbol(N,K_/L,T,a)

//Функция решения гиперболического уравнения с помощью явной разностной схемы. Входные данные: N - количество участков разбиения интервала (0,L); K - количество участков разбиения интервала (0,T); a - коэффициент теплопроводности; u - матрица решений в узлах сетки; массив x; массив t,

// Вычисляем шаг по х и по t

h=L/N; delta=T/K;

//Формируем массив x, первый и второй столбцы матрицы решений u из начального условия

for i=1:N+1

x(i)=(i-1)*h;

u(i,1)=fi(x(i));

u(i,2)=u(i,1)+delta*psi(x(i));

end

//Формируем массив t, первую и последнюю строки матрицы решений u из граничных условий

for j=1:K+1

t(j)=(j-1)*delta;

end

//Формируем первую и последнюю строки матрицы решений u из граничных условий

for j=2:K+1

u(1,j)=0;

u(N+1,j)=fi(L);

end

gam=a^2*delta^2/h^2;

//Формируем матрицу решений u

for j=2:K

for i=2:N

u(i,j+1)=-u(i,j-1)+gam*u(i-1,j)+(2-2*gam)*... u(i,j)+gam*u(i+1,j)+delta^2*f(x(i),t(j));

end

end

end

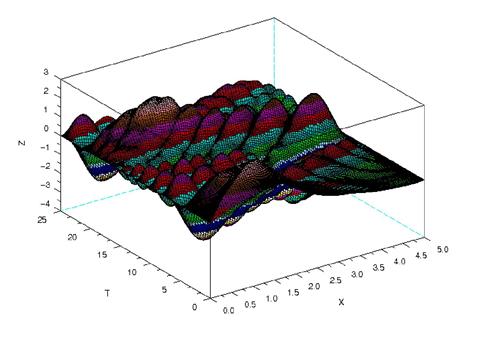
Рис.1.4. График решения гиперболического уравнения