Кручение. Крутящий момент. Построение эпюр

Кручением называется такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент М_к.

Кручение бруса вызывают скручивающие (вращающие) моменты М (или Т), действующие в плоскостях, перпендикулярных оси бруса (рисунок 144).

Брус, нагруженный вращающими моментами, называется валом.

Во всех машинах и механизмах имеются валы с укрепленными на них различными деталями: зубчатыми колесами, шкивами ременных передач, звездочками цепных передач и т.д., передающими вращающие моменты.

При равномерном вращении вала сумма вращающих моментов, действующих на вал, равна нулю .

Рисунок 144

При известных передаваемой мощности Р (Вт) и угловой скорости вала ω (рад/с) вращающий момент М (Н·м) можно определить по формуле

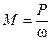
Если известна частота вращения вала n , то его угловая скорость

.

Для определения крутящего момента применяют метод сечений и рассматривают равновесие оставшейся части: ; , т.е. при

простом нагружении , при сложном нагружении

(87).

v Крутящий момент в сечении бруса равен алгебраической сумме внешних моментов, приложенных по одну сторону от сечения.

Внешние моменты будем считать положительными, если они вращают оставшуюся часть по часовой стрелке, при этом смотреть надо на сечение оставшейся части со стороны отброшенной.

Если на брус действует несколько внешних (вращающих) моментов, то для определения опасного сечения или участка вала строят эпюры крутящих моментов М_к аналогично эпюрам продольных сил.

Пример 38. Построить эпюру крутящих моментов для вала (рисунок 145).

Дано: М₁ = 10 кН·м; М₂ = 35 кН·м; М₃ = 20 кН·м; М₄ = 5 кН·м.

Вал проще показывать схемой рисунка 145-б, что и будем делать в дальнейшем.

Решение

1) Разбиваем брус между моментами на четыре участка.

2) Нумеруем участки с любого конца с I по IV.

3) Для каждого участка, используя метод сечений, определяем крутящий момент

Определение М_к1 и М_к2 показано в таблице 15.

Рисунок 145

Таблица 15

Участок	Оставшаяся часть	Мк
I		Мк1 = М1 = 10 кН·м (смотрим справа)
II		Мк2 = М1 – М2 = 10 – 35 = -25 кН·м (смотрим справа)

М_к3 = М₁ – М₂ + М₃ = 10 – 35 + 20 = -5 кН·м;

М_к4 = М₁ – М₂ + М₃ + М₄ = 10 – 35 + 20 + 5 = 0.

4) Строим в масштабе эпюру М_к (рисунок 141-в).

5) Определяем наиболее нагруженный участок (без учета знака) – II, т.е. М_{к max} = 25 кН·м.

6) Проверка (устная):

Под внешним моментом на эпюре крутящих моментов будет вертикальный скачок, равный по величине этому моменту.

Подумай и ответь на вопросы

83 Можно ли считать, что алгебраическая сумма вращающих моментов равна нулю, если вал вращается с постоянной угловой скоростью?

1) Можно; 2) Нельзя.

84 Укажите какие участки вала (рисунок 146) скручиваются.

1) Все участки вала; 2) Только участок между шкивами.

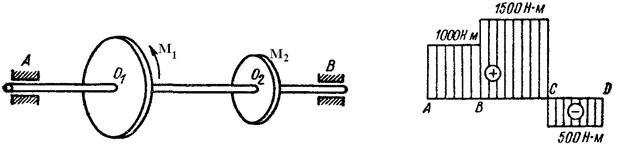
Рисунок 146 Рисунок 147

85 На рисунке 147 показана эпюра крутящих моментов. Чему равно максимальное значение крутящего момента, по которому нужно рассчитывать вал на прочность?

1) 1000 Н·м; 2) 1500 Н·м; 3) 500 Н·м.

86 На эпюре крутящих моментов отмечены (рисунок 147) точки А, В, С, D, соответствующие сечениям вала, где установлены шкивы (колеса). Какая точка соответствует сечению, где установлен ведущий шкив, и чему равен вращающий момент, на этом шкиве?

1) В сечении В; М_max = 1500 Н·м;

2) В сечении С; М_max = 1500 Н·м;

3) В сечении С; М_max = 2000 Н·м.

87 По заданной эпюре крутящих моментов (рисунок 148) составить схему нагружения вала.

Рисунок 148