Имеющих ось симметрии

v Момент инерции сложного сечения относительно некоторой оси равен сумме моментов инерции составных частей сечения относительно этой оси.

Пример 36. Определить главные моменты инерции сечения (рисунок 139).

Решение

Определяем координаты центра тяжести сечения С. Так как сечение имеет ось симметрии и на ней расположен центр тяжести, то необходимо определить только одну координату у_С. Проводим вспомогательную ось перпендикулярную оси симметрии, являющейся главной осью инерции у. Разбиваем сечение на два прямоугольника. Ордината центра тяжести сечения

Рисунок 139

.

Проводим главную центральную ось сечения х и определяем по формуле (85) моменты инерции прямоугольников относительно этой оси

;

.

Аналогично определяем моменты инерции прямоугольников относительно оси у (заметим, что ось у – главная центральная ось обоих прямоугольников, так как является их осью симметрии)

; .

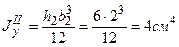Вычисляем главные центральные моменты инерции сечения:

;

.

Пример 37. Определить главные центральные моменты инерции сечения, составленного из двух швеллеров № 18 (рисунок 141).

Решение

1 Сечение, составленное из профилей двух швеллеров, имеет две оси симметрии, с которыми и совместим главные оси х и у.

2 Ось х является главной центральной осью каждого из двух швеллеров. Поэтому для определения главного центрального момента инерции сечения относительно этой оси достаточно сложить моменты каждого из профилей относительно той же оси.

Рисунок 140 Рисунок 141.

По таблицам ГОСТ 8240-89 находим J_Ix = J_2x = 1090 см⁴.

Момент инерции всего сечения относительно оси х

J_x = J_Ix + J_2x = 2 · 1090 = 2180 см⁴.

3 Главная центральная ось сечения у параллельна осям С₁у₁ и С₂у₂ (рисунок 141) – главным центральным осям каждого из профилей 1 и 2. Для определения главного момента инерции сечения воспользуемся формулой (85):

,

где (по ГОСТ 8240-89) J_Iу = J_2у = 86 см⁴; расстояние между осями а₁ = а₂ = b – z₀ = = 7 – 1,94 = 5,06 см; площади профилей А₁ = А₂ = 20,7 см². Следовательно,

.

4 Главные центральные моменты инерции сечения

J_max = J_x = 2180 см⁴ и .

82 Вычислите главные центральные моменты инерции сечения, составленного их двух швеллеров № 20 (рисунок 142).

Рисунок 142