Разложение некоторых элементарных функций в ряд Маклорена

1. . Для этой функции , .

По формуле (3.2) составим ряд Маклорена данной функции:

. (3.3)

Найдем радиус сходимости ряда (3.3) по формуле (1.3):

.

Следовательно, ряд (3.3) сходится при любом значении .

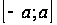Все производные функции на любом отрезке ограничены, т. е.

.

Поэтому, согласно теореме 3.1, имеет место разложение

. (3.4)

2. . Для этой функции , , .

Отсюда следует, что при производные четного порядка равны нулю, а производные нечетного порядка чередуют знак с плюса на минус.

По формуле (3.2) составим ряд Маклорена:

.

При любом фиксированном значении этот ряд сходится как знакочередующийся по признаку Лейбница. При этом

.

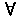
Поэтому, согласно теореме 3.1, имеет место разложение

. (3.5)

3. . Воспользуемся разложением (3.5) в ряд Маклорена функции и свойством 2 о дифференцировании степенного ряда. Имеем

.

(3.6)

Поскольку при почленном дифференцировании интервал сходимости степенного ряда не изменяется, то разложение (3.6) имеет место при любом .

Приведем без доказательства разложения других элементарных функций в ряды Маклорена.

4.

– биномиальный ряд ( – любое действительное число).

Если – положительное целое число, то получаем бином Ньютона:

.

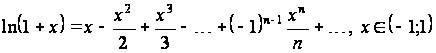– логарифмический ряд.

.