 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства степенных рядов
|
|
Степенной ряд (1.2) представляет собой функцию 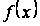 , определенную в интервале сходимости
, определенную в интервале сходимости 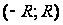 , т. е.
, т. е.
 .
.
Приведем несколько свойств функции 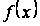 .
.
Свойство 1. Функция 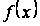 является непрерывной на любом отрезке
является непрерывной на любом отрезке 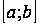 , принадлежащем интервалу сходимости
, принадлежащем интервалу сходимости 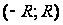 .
.
Свойство 2. Функция 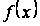 дифференцируема на интервале
дифференцируема на интервале 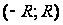 , и ее производная
, и ее производная  может быть найдена почленным дифференцированием ряда (1.2), т. е.
может быть найдена почленным дифференцированием ряда (1.2), т. е.
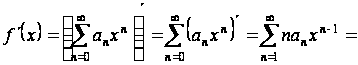
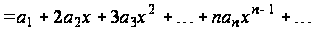 ,
,
для всех 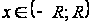 .
.
Свойство 3. Неопределенный интеграл от функции 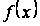 для всех
для всех 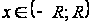 может быть получен почленным интегрированием ряда (1.2), т. е.
может быть получен почленным интегрированием ряда (1.2), т. е.
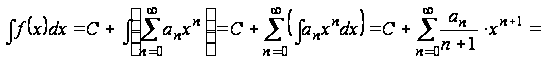
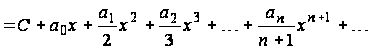
для всех 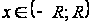 .
.
Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала 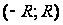 может измениться.
может измениться.
Приведенные свойства справедливы также и для степенных рядов (1.1).
Пример 2.1. Рассмотрим степенной ряд
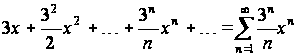 .
.
Область сходимости этого ряда, как показано в примере 1.1, есть промежуток 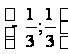 .
.
Почленно продифференцируем этот ряд:
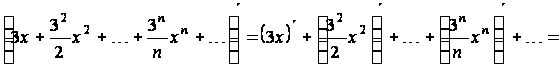
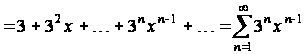 .(2.1)
.(2.1)
По свойству 2 интервал сходимости полученного степенного ряда (2.1) есть интервал 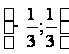 .
.
Исследуем поведение этого ряда на концах интервала сходимости, т. е. при 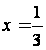 и при
и при 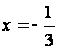 .
.
При 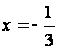 степенной ряд (2.1) превращается в числовой ряд
степенной ряд (2.1) превращается в числовой ряд
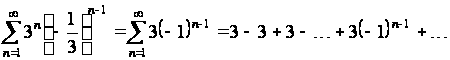 .
.
Этот числовой ряд расходится, так как не выполняется необходимый признак сходимости 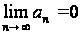 :
:  , который не существует.
, который не существует.
При 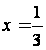 степенной ряд (2.1) превращается в числовой ряд
степенной ряд (2.1) превращается в числовой ряд
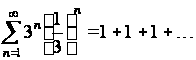 ,
,
который также расходится, так как не выполняется необходимый признак сходимости.
Следовательно, область сходимости степенного ряда, полученного при почленном дифференцировании исходного степенного ряда, изменилась и совпадает с интервалом 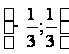 .
.
Дата публикования: 2015-10-09; Прочитано: 219 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
