 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение краевой задачи
|
|
ВАРИАНТЫ ЗАДАНИЙ
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор


Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 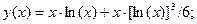
- Решить задачу Коши методом Предиктор-Корректор


Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:

Точное решение: 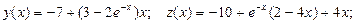
- Решить задачу Коши методом Рунге-Кутта-Фельберга
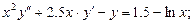

Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:

Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:
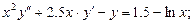

Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:

Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:

Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:

Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 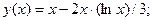
- Решить задачу Коши методом Предиктор-Корректор:

Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:

Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:


Точное решение: 
- Решить задачу Коши методом Рунге-Кутта-Фельберга


Точное решение: 
- Решить задачу Коши методом Предиктор-Корректор:


Точное решение: 
РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Каждый студент получает свое задание на одну из трех тем. Студент должен создать программу решения на языке Mathcad и провести расчеты.
Для получения зачета студент должен продемонстрировать на экране компьютера действующую программу, реализующую решение поставленных задач. Студент должен уметь объяснить все детали представленной программы и ответить на связанные с темой теоретические вопросы.
1. Решение линейной краевой задачи методом редукции к задачам Коши
Найти решение дифференциального уравнения на отрезке [a,b] с заданным значением шага приращения аргумента h = (b-a)/n. Для решения возникающих задач Коши использовать метод Рунге–Кутта четвертого порядка. Построить совмещенный график точного и приближенного решений. Построить график погрешности решения. Проверить, как меняется погрешность при изменении шага приращения аргумента.
2. Решение линейной краевой задачи методом конечных разностей
Найти решение дифференциального уравнения на отрезке [a,b] с заданным (h = (b-a)/n) и с половинным (h/2) значением шага приращения аргумента. Построить совмещенные графики решений с шагом h и с шагом h/2, точного решения и решения, уточненного по правилу Рунге. Построить совмещенные графики оценки погрешности и истинной погрешности для решений с шагом h и h/2, и уточненного решения. Проверить, как меняется погрешность при изменении шага приращения аргумента.
Дата публикования: 2015-10-09; Прочитано: 436 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
