В.1. Вывод граничных условий для касательных составляющих векторов напряженности магнитного поля

Рассмотрим произвольную точку границы раздела (S) двух изотропных сред. Проведем в этой точке из второй среды в первую единичную нормаль (см. рис. В.2). Рассмотрим плоскость , проходящую через нормаль . На линии пересечения границы раздела и плоскости выделим достаточно малый отрезок так, чтобы выбранная точка находилась внутри этого отрезка. Размеры этого отрезка должны быть такими, чтобы его можно было считать прямолинейным, и чтобы в обеих средах вектор можно было считать постоянным в пределах . В плоскости на отрезке построим прямоугольный контур высоты так, чтобы одна его часть находилась в первой, а вторая – во второй среде. Проведем в выбранной точке орты и . Орт направлен по касательной к отрезку , а орт направлен по нормали к плоскости и так, чтобы выполнялось соотношение

. (В.5)

Рассмотрим первое уравнение Максвелла в интегральной форме

.

Подставим в это уравнение формулу (1.2) для тока , тогда оно принимает следующий вид:

. (В.6)

Отметим, что в уравнении (В.6) контур является произвольным, а поверхность 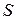должна быть такой, чтобы ее края совпадали с контуром . Принято говорить, что поверхность 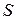опирается на контур .

Внесем в (В.6) производную по времени под знак интеграла и запишем уравнение (В.6) для контура , тогда получим, что

, (В.7)

где – площадь, охватываемая контуром , а .

Представим левую часть равенства (В.7) в виде суммы четырех интегралов

. (В.8)

Устремим в (В.8) высоту контура к нулю так, чтобы стороны и оставались в разных средах и в пределе совпали с отрезком , тогда второе и четвертое слагаемые в (В.8) стремятся к нулю (к нулю стремятся пределы интегрирования, а подынтегральные функции конечны). В этом случае соотношение (В.8) принимает следующий вид:

, (В.9)

где и – векторы напряженности магнитного поля на отрезке со стороны первой и второй среды.

Учитывая, что , и тот факт, что вектор можно считать постоянным в пределах отрезка , получаем следующее равенство:

. (В.10)

Учтем в последнем равенстве, что , тогда

. (В.11)

Вычислим теперь правую часть соотношения (В.7) при . Очевидно, что при этом . Учтем, что величина является всегда ограниченной величиной. Рассмотрим случай, когда граница раздела не является поверхностью идеального проводника. В этом случае объемная плотность тока проводимости также является ограниченной величиной и

. (В.12)

Подставим равенства (В.11) и (В.12) в соотношение (В.7), тогда получаем, что

.

Учитывая свойство скалярного произведения и тот факт, что , получаем следующее соотношение

. (В.13)

Сравнивая соотношения (В.13) и второе соотношение (В.1), видим, что для рассматриваемого случая, когда объемная плотность тока проводимости ограничена, а значит когда , они совпадают.

Пусть теперь . Это соответствует случаю, когда граница раздела является поверхностью идеального проводника. В этом случае

.

Подставим последнее равенство и равенство (В.11) в соотношение (В.7), тогда получаем, что

. (В.14)

Сократим равенство (В.14) на . Учитывая свойство скалярного произведения и тот факт, что , получаем следующее соотношение

.

Последнее соотношение совпадает со вторым соотношением в формуле (В.1). Отметим, что оно является общим видом граничного условия для касательных составляющих вектора напряженности магнитного поля. В случае, когда , оно совпадает с условием (В.13).

Получим теперь векторную форму граничного условия. Для этого учтем очевидное равенство . Подставляя это равенство в (В.14), получаем, что

.

Учитывая свойства смешанного произведения трех векторов, можно записать, что

.

Поскольку последнее равенство справедливо при любом направлении орта , которое определяется ориентацией контура , то из него следует, что

. (В.15)

Последнее равенство совпадает с первым соотношением формулы (В.1). Это равенство является векторной формой записи граничного условия для касательных составляющих векторов напряженности магнитного поля.