А.1. Вывод закона полного тока в дифференциальной форме

Запишем первое уравнение Максвелла в интегральной форме.

. (А.1)

Внесем в уравнении (А.1) производную по времени, т.е. величину , под знак интеграла. Это допустимо, так как интегрирование проводится по пространственным координатам. Тогда уравнение (А.1) с учетом формулы (1.2) примет следующий вид:

. (А.2)

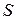Напомним формулировку закона полного тока в интегральной форме: циркуляция вектора напряженности магнитного поля по любому замкнутому контуру L равна полному току, протекающему через любую поверхность, опирающуюся на этот контур. Отсюда следует, что контур и поверхность в уравнении (А.2) жестко связаны между собой.

Воспользуемся теоремой (формулой) Стокса (см. приложение Е)

,

которая утверждает, что циркуляция произвольного вектора по любому замкнутому контуру L равна потоку вихря этого вектора через любую поверхность, опирающуюся на этот контур.

Подставим формулу Стокса в соотношение (А.2), тогда можно записать, что

.

Последнее равенство можно записать в следующем виде:

. (А.3)

Из формулировки первого уравнения Максвелла в интегральной форме следует, что равенство (А.3) должно выполняться для произвольной поверхности S. Отсюда следует, что для выполнения равенства (А.3) необходимо, чтобы выражение под интегралом в (А.3) было равно нулю в любой точке пространства, т.е. чтобы выполнялось следующее равенство:

или

. (А.4)

Равенство (А.4) является математической формулировкой закона полного тока в дифференциальной форме.