Вывод граничных условий для векторов электромагнитного поля

Как отмечалось в подразд. 1.5, уравнения Максвелла в дифферен­циальной форме не пригодны на границе раздела двух сред. Это связано с тем, что при переходе через границу раздела двух сред векторы электромагнитного поля испытывают скачкообразные изменения. Соотношения между векторами в двух очень близких точках, находящихся по обе стороны границы раздела двух сред, называются граничными условиями. Граничные условия являются следствием уравнений Максвелла в интегральной форме и определяются равенствами следующего вида:

, , (В.1)

, , (В.2)

, , (В.3)

, , (В.4)

где – нормаль к границе раздела S, направленная из второй среды в первую, 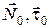– векторы, лежащие в плоскости Р, которая является касательной к границе раздела. При этом (см. рис. В.1)

Рисунок В.1 – К пояснению граничных условий

Равенства (В.1) и (В.2) определяют граничные условия для касательных составляющих вектора напряженности магнитного и электрического поля, а равенства (В.3) и (В.4) – для нормальных составляющих векторов электрической и магнитной индукции. Первая формула в этих равенствах дает векторную форму граничного условия, а вторая – скалярную форму.

Настоящее приложение посвящено выводу граничных условий.