В.3. Вывод граничных условий для нормальных составляющих векторов электрической индукции

Рассмотрим произвольную точ­ку границы раздела (S) двух изотроп­ных сред. Проведем в этой точке из второй среды в первую единичную нормаль (см. рис. В.3). Выберем в окрестности этой точки достаточно малую поверхность так, чтобы ее можно было считать плоской, и чтобы в обеих средах вектор 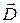можно было считать постоянным в пределах . Построим на элементе прямой цилиндр высотой так, чтобы его основания находились в разных средах.

Рассмотрим третье уравнение Максвелла в интегральной форме

. (В.17)

Подставим в это уравнение соотношение (1.1), связывающее заряд и его объемную плотность , тогда

. (В.18)

Отметим, что в уравнении (В.18) замкнутая поверхность 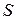, ограничивающая объем , является произвольной.

Запишем уравнение (В.18) для поверхности цилиндра, указанного выше, тогда получим, что

. (В.19)

Представим интеграл в левой части равенства (В.19) в виде суммы интегралов по основаниям цилиндра и его боковой поверхности. Учитывая, что основания цилиндра находятся в разных средах, получаем следующее соотношение:

, (В.20)

где и векторы, направленные вдоль внешних нормалей к соответствую­щим основаниям цилиндра.

Устремим в (В.20) высоту цилиндра к нулю так, чтобы основания и оставались в разных средах и в пределе совпали с элементом . Тогда, учитывая, что третье слагаемое в (В.20) стремятся к нулю (к нулю стремится площадь боковой поверхности при ограниченной подынтегральной функции), получаем следующее равенство:

, (В.21)

где и – векторы электрической индукции на элементе со стороны первой и второй среды.

Учитывая, что , и тот факт, что векторы и можно считать постоянными в пределах элемента , получаем следующее равенство:

. (В.22)

Учтем в последнем равенстве то, что , тогда

. (В.23)

Вычислим теперь правую часть соотношения (В.19) при . При этом объем цилиндра стремиться к нулю (). Рассмотрим случай, когда граница раздела является поверхностью идеального проводника. В этом случае на поверхности проводника распределен поверхностный заряда, т.е. .

.

Подставим последнее равенство и равенство (В.23) в соотношение (В.9), тогда получим, что

.

Сократим последнее равенство на , тогда получим следующее соотношение

. (В.24)

Соотношение (В.24) совпадает с первым соотношением в формуле (В.3).

Учитывая свойство скалярного произведения и тот факт, что , получаем следующее соотношение

. (В.25)

Последнее соотношение совпадает со вторым соотношением в формуле (В.3), т.е. определяет граничное условие в скалярной форме. Отметим, что соотношения (2.24) и (2.25) определяют граничное условие (в векторной и скалярной форме) для нормальных составляющих вектора электрической индукции в общем случае. В случае, когда граница раздела двух сред не является идеальным проводником, то в этих соотношениях надо положить .