 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие отношения
|
|
В математике изучают не только сами объекты (числа, фигуры, величины), но и связи, отношения между ними. Так, усвоение понятия натурального числа — одного из ведущих понятий начальной математики и математики вообще — происходит благодаря изучению различных взаимосвязей между числами. Например, выясняется, что:
число 5 больше числа 2;
число 10 больше числа 8 на 2;
число 7 следует за числом 6, т. е. числа связаны различными отношениями: «больше», «больше на», «следует за» и др.
В геометрии изучают параллельность и перпендикулярность прямых, равенство и подобие фигур, т. е. различные отношения между геометрическими объектами.
Сравнивая множества, мы говорим, например, что они пересекаются, или равны, или одно включено в другое, т. е. устанавливаем отношения между множествами.
В математике чаще всего рассматривают отношения между двумя объектами. Их называют бинарными. В нашем курсе мы будем изучать только такие отношения, поэтому в дальнейшем слово «бинарные» будем опускать.
Перед нами стоит задача: разом можно классифицировать такое огромное число самых разнообразных отношений. Знание этого материала нужно учителю начальных классов для того, чтобы, изучая конкретные отношения в начальной школе имея представления о конкретных отношениях между числами, геометрическими фигурами, множествами и другими объектами, установить, что общего у этих отношений, каким об начальной школе, понимать их общность, взаимосвязи, роль в усвоении тех или иных понятий.
Выясним сначала, что общего у различных отношений.

(5, 4), (6, 5)), а для отношения «меньше в 2 раза» — множество, содержащее две пары: ((3, 6), (4, 8)}. Таким образом, можно сказать, что каждое из рассматриваемых отношений определяется множеством пар чисел, образованных из элементов множества Х = {3, 4, 5, 6. 8}.
Известно, что упорядоченные пары — это элементы декартова произведения множеств или его подмножеств. Нетрудно видеть, что те множества пар, которые определяют отношения «больше», «больше на 1» и «меньше в 2 раза», являются подмножествами декартова произведения ХХХ = {(3, 3), (3, 4), (3, 5), (3, 6), (3, 8), (4, 3), (4, 4), (4, 5), {4, 6), (4, 8), (5, 3), (5, 4), (5, 5), (5, 6), (5, 8), (6, 3), (6, 4), (6, 5), (6, 6), (6, 8), (8, 3), (8, 4), (8, 5), (8, 6), {8, 8)}.
Итак, каждое из рассматриваемых отношений определяется множеством пар, которое, в свою очередь является подмножеством декартова произведения X 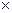 X.
X.
Вместо того чтобы говорить, что отношение определяется множеством пар, в математике само это множество пар называют отношением между элементами множества X.
Определение. Отношением между элементами множества X или отношением на множестве X называется всякое подмножество декартова произведения X 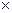 X.
X.
Отношения обозначают прописными буквами латинского алфавита: Р, Q, R, S и др. Следовательно, если R — отношение между элементами множества X, то R 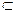 X
X 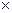 X.
X.
Отношения на конечном множестве X можно представлять наглядно, при помощи особых чертежей, состоящих из точек, соединенных стрелками. Такие чертежи называют графами.
Построим, например, граф отношения «больше» между элементами множества Х = {2, 4, 6, 8, 12. Для этого элементы данного множества изобразим точками и соединим стрелками те точки, которые изображают числа, находящиеся в отношении «больше». Поскольку 4>2, то проводим стрелку от 4 > 2; так как 6>4, то проводим стрелку от 6>4 и т. д., пока не переберем все пары чисел, связанных заданным отношением. В результате получаем граф отношения «больше» для элементов множества Х = {2, 4, 6, 8, 12} (рис. 56).
 Рассмотрим теперь на том же множестве X отношение «кратно» и построим его граф. Аналогично предыдущему случаю изобразим элементы множества X точками и соединим стрелками те, которые изображают числа, находящиеся в отношении «кратно»: 12
Рассмотрим теперь на том же множестве X отношение «кратно» и построим его граф. Аналогично предыдущему случаю изобразим элементы множества X точками и соединим стрелками те, которые изображают числа, находящиеся в отношении «кратно»: 12

Дата публикования: 2015-09-18; Прочитано: 1879 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
