Методичні вказівки. Розв`язання задачі. Дано координати вершин піраміди А(1;-1;2), В(1-β; 3+β;2-β), С(1;3;-3)

Розв`язання задачі. Дано координати вершин піраміди А(1;-1;2), В(1-β; 3+β;2-β), С(1;3;-3), D(1;-5;1). Візьмемо β=3, тоді координати вершин піраміди АВСD будуть такі: A(1;-1;2), В(-2;6;-1), С(1;3;-3), D(1;-5;1).

Побудуємо схематичний малюнок піраміди, не привязуючись до системи координат OXYZ.

D

В

А

C

1. Довільний вектор можна записати в системі орт за слідуючою формулою: (1)

- проекції вектора на координатні осі 0x, 0y та 0z; - одиничні вектори, які направлені так, як направлені осі 0x, 0y та 0z. Якщо задані точки та , то проекції вектора на координатні осі знаходяться за формулами:

(2)

Тоді:

(3)

Підставляючи в (3) координати точок А та В, одержимо вектор

Аналогічно, підставляючи в (3) координати точок А та С, знаходимо вектор

Підставляючи в (3) координати точок А та D, одержимо вектор

Отже знайдені вектори мають такі координати:

.

Якщо вектор задано формулою (1), або (3), то його модуль (довжина) обчислюється за формулою:

Застосовуючи цю формулу, обчислюємо модулі знайдених векторів :

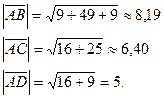
2. Так як скалярний добуток двох векторів , дорівнює добутку їх довжин, помноженому на косинус кута мім ними, тобто:

то косинус кута φ між двома векторами , дорівнює скалярному добутку цих векторів, поділеному на добуток їх модулів:

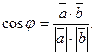(4)

Якщо координати векторів-співмножників відомі ), то їх скалярний добуток можна знайти за формулою:

(5)

Знаходимо скалярний добуток векторів за формулою (5):

Отже за формулою (4) дістанемо:

сosφ = cosA =

3. Проекція вектора на знаходиться за формулою:

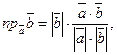звідки

Отже проекція вектора на дорівнює скалярному добутку цих векторів, поділеному на модуль вектора :

(лін. од.)

4. Площа грані АВС дорівнює половині площі паралелограма, побудованого на векторах . Позначимо векторний добуток вектора на вектор через вектор :

.

В M

А С

Тоді, виходячи з геометричного змісту модуля векторного добутку двох векторів, величина модуля вектора чисельно дорівнює площі паралелограма, побудованого на векторах 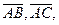а площа грані АВС буде чисельно дорівнювати половині модуля вектора :

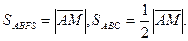
Знайдемо векторний добуток векторів :

= =

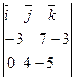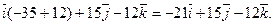
Таким чином, (-21;15;-12), а його модуль дорівнює:

.

Отже (кв.од.)

5. Об`єм паралелепіпеда, побудованого на трьох некомпланарних векторах чисельно дорівнює абсолютній величині їх мішаного добутку:

.

А об`єм піраміди дорівнює шостій частині від об`єму паралелепіпеда:

.

Обчислимо мішаний добуток:

= =-3(12-20)=24

Отже V паралелепіпеда дорівнює V=24 куб.од., а об`єм піраміди ABCD V= 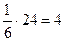(куб.од.).

Тепер можна знайти висоту DК піраміди ABCD:

,звідки

тому DК (лін.од.).

Отже висота DК заданої піраміди дорівнює 0,8 лін.одиниць.

6 Знайдемо кут α нахилу бічного ребра AD до площини основи АВС.

З трикутника АВК: α =90- φ, тому sinα = sin(90- φ) = cosφ.

Кут φ - це кут між векторами і вектором , перпендикулярним до площини основи: (0,4,-5), (-3,7,-3).

=

(23,15,12).

Знайдемо координати вектора : (0,-4,-1).

Тоді

sinα = cosφ =

7 Кут α нахилу площини бічної грані (ADC) до площини основи ((АВС) буде дорівнювати куту між векторами , що відповідно перпендикулярні до цих площин.

Для знаходження вектора , в площині (ADC) знайдемо координати двох векторів, що лежать в цій площині:

(0,-4,3), (0,4,-5).

Тоді = Тобто (8,0,0).

Аналогічно, =

Значить, (23,15,12).

Тоді за формулою cosα =

Маємо:

cosα = .

Відповіді:

5.

7.

8.

9.

10.

11.

12. З векторів можна скласти трикутник, який задовольняє умовам задачі лише в тому випадку, коли мас місце одне знаступних співвідношень:

, Використовуючи координати век­торів, переконуємося у тому, що для них виконане третє співвідношення.

13. Так як , то трапеція АВСD існує.

14.

15.

16.

17.

18.

20.

21. Сума квадратів діагоналей паралелограма дорівнює сумі квадра­тів його сторін.

22.

23.

25.

26.

28.

29. z=

30. N(4;1;1).

31.

32. 1)Може; 2)не може; 3)може.

33.

34.

35. 1)Вектори мають бути взаємно перпендикулярні; 2)кут віж векторами має бути гострим; 3)кут між векторами має бути тупим.

38. |R|=15.

39. α = 4, β = -1.

40. Вектор у два рази довший за вектор ; вони напрямлені у одну сторону.

41. .

42. .

43. середини сторін трикутника АВС.

44. .

45.

46. 1)10; 3)0; 4)-6.

47. 1)5; 2)3.

48. 1)-62, 2)162, 3)373.

49. Сума квадратів діагоналей паралелограма рівна сумі квадратів його сторін.

50.

51. .

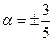52.

53.

54. 1)22, 2)6, 3)7, 4)-200, 5)129, 6)41.

55.

57.

58. -3.

59. 3.

60. 2) 3)[ ]=(20;-20;-10); 4)[ ]=(-38;26;21).

61. |[ ]| = 16.

62. 1)24; 2)60.

64. 1)(5;7;1), 2)(10;2;14), 3)(20;4;28).

65. 1)(6;-4;-6), 2)(-12;8;12).

66. 14 кв. од.

67. 5.

68. .

69.

70.

72. Доведення.

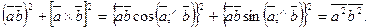
73. [ ] = (-27;27;-27),

74. |[ ]| = 28,

75. 1)права, 2)ліва, 3)ліва, 4)права, 5)вектори компланарні, 6)ліва.

76. 1)46; 2)-30; 3)18; 4)-9.

77.

79.

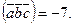
80. 1)компланарні; 2)не компланарні; 3)компланарні.

82. 3 куб. од.

83. 11.

84.

85.

86.

87.

88. -1,5.

90. 1)23[ ]; 2)47[ ] + 4[ ] - 38[ ]; 3) .

92. 1)так; 3)ні; 4)так.

93. 1)13; 2)76; 3)12; 4)0.

94. 1)23/3; 2)62/3.