 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Розв’язання 2
|
|
Якщо одиничні взаємно перпендикулярні вектори 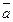 і
і  прийняти за координатні орти прямокутної декартової системи координат Oxy, то у цій системі координат вектори
прийняти за координатні орти прямокутної декартової системи координат Oxy, то у цій системі координат вектори 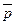 і
і  будуть мати наступні координати:
будуть мати наступні координати: 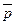 =(3,2),
=(3,2),  =(1,5).
=(1,5).
Тоді:

|
Відповідь:

|
9. Початок вектора знаходиться в точці М(4,-3,5), кінець - в точці N(6,-2,3). Знайти координати вектора  , його довжину та направляючі косинуси.
, його довжину та направляючі косинуси.
Розв`язання. Позначимо координати вектора  через X, Y, Z. Знаходимо:
через X, Y, Z. Знаходимо:  ,
,  ,
,  , тобто
, тобто  (2,1,-2).
(2,1,-2).
Довжина вектора:  .
.
Знаходимо направляючі косинуси:

Відповідь:  (2,1,-2).
(2,1,-2). 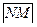 = 3
= 3

10. Дано вектори 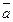 (1,1,-1),
(1,1,-1),  (2,-1,3),
(2,-1,3), 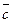 (1,-2,1). Розкласти вектор
(1,-2,1). Розкласти вектор 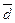 (12,-9,11) по векторам
(12,-9,11) по векторам 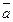 ,
,  ,
, 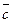 .
.
Розв`зання: Нехай  - деякі коефіцієнти. Так як рівні вектори мають рівні координати, а координати лінійної комбінації векторів рівні відповідним лінійним комбінаціям однойменних координат, то
- деякі коефіцієнти. Так як рівні вектори мають рівні координати, а координати лінійної комбінації векторів рівні відповідним лінійним комбінаціям однойменних координат, то
 12 = α + 2β + γ,
12 = α + 2β + γ,
-9 = α - β - 2γ, Із системи знайдемо: α=2, β=3, γ=4.
11 = -α +3β + γ.
Отже, 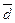 =2
=2 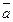 +3
+3  +4
+4 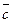 .
.
Відповідь: 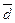 =2
=2 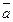 +3
+3  +4
+4 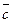 .
.
11. Дано чотирикутник з вершинами А(7,-8,4), В(7,4,-2), С(-5,10,-2), D(-5,-2,4). Довести, що його діагоналі АС і ВD взаємно перпендикулярні.
Розв`язання. Для доведення достатньо знайти координати векторів  і
і  , виразити їх скалярний добуток в координатах та переконатися у виконанні рівності
, виразити їх скалярний добуток в координатах та переконатися у виконанні рівності 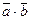 =0 чи
=0 чи  . Знаходимо:
. Знаходимо:  =(-12,18,-6),
=(-12,18,-6),  =(-12,-6,6).
=(-12,-6,6).
Так як  =(-12)(-12)+18(-6)+(-6)6=144-108-36=0, то
=(-12)(-12)+18(-6)+(-6)6=144-108-36=0, то  ┴
┴  , що і треба було довести.
, що і треба було довести.
12. Який кут утворюють одиничні вектори  та
та  , якщо відомо, що вектори
, якщо відомо, що вектори 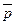 =3
=3  +6
+6  та
та  =10
=10  -8
-8  взаємно перпендикулярні?
взаємно перпендикулярні?
Розв`язання. Оскільки 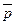 ┴
┴  , то
, то  =0. Знайдемо вираз для скалярного добутку, користуючись його властивостями:
=0. Знайдемо вираз для скалярного добутку, користуючись його властивостями:
 =(3
=(3  +6
+6  )(10
)(10  - 8
- 8  )=
)=  .
.
За умовою  , тому
, тому  Далі, за означенням
Далі, за означенням  шуканий кут між векторами
шуканий кут між векторами  та
та  . Звідси,
. Звідси,  Відповідь:
Відповідь: 
13. Дано трикутник з вершинами А(-1,1,5), В(3,-4,5), С(-1,5,2). Знайти довжину висоти, опущеної з вершини В на сторону АС.
Розв`язання. Щоб розв`язати задачу, достатньо знайти площу трикутника АВС та довжину сторони АС. Площа трикутника АВС рівна половині площі паралелограма, що побудований на векторах  та
та  . Знайдемо координати цих векторів та координати їх векторного добутку:
. Знайдемо координати цих векторів та координати їх векторного добутку:  =(4,-5,0),
=(4,-5,0),  =(0,4,-3),
=(0,4,-3),
[ 
 ]=
]=  . Оскільки |[
. Оскільки |[ 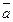
 ]|=S, то знаходимо площу паралелограма: S=|[
]|=S, то знаходимо площу паралелограма: S=|[ 
 ]|=
]|=  Так як
Так як 
звідки  .
.
Відповідь:  .
.
14. Сила  прикладена до точки М(3,4,-2). Знайти величину та направляючі косинуси моменту цієї сили відносно початку координат.
прикладена до точки М(3,4,-2). Знайти величину та направляючі косинуси моменту цієї сили відносно початку координат.
Розв`язання. Якщо  , то [
, то [  ] - момент сили F відносно точки О. Застосовуючи формули
] - момент сили F відносно точки О. Застосовуючи формули  отримаємо [
отримаємо [  ]=(20,-4,22). Отже, [
]=(20,-4,22). Отже, [  ]=
]=  ;
;

Відповідь:  F=30.
F=30.
15. Дано три вектори  ,
,  ,
,  . Знайти мішаний добуток ((
. Знайти мішаний добуток (( +
+  )(
)( +
+  )(
)( +
+  )).
)).
Розв`язання. Скориставшись властивостями мішаного добутку, отримаємо:
(( +
+  )(
)( +
+  )(
)( +
+  ))=((
))=(( +
+  )(
)( +
+  )
)  )+((
)+(( +
+  )(
)( +
+  )
)  )=
)=
=(( +
+  )
) 
 )+((
)+(( +
+  )
) 
 )+((
)+(( +
+  )
) 
 )+((
)+(( +
+  )
) 
 )=
)=
=(

 )+(
)+(

 )+(
)+(

 )+(
)+(

 )+(
)+(

 )+(
)+(

 )+(
)+(

 )+(
)+(

 ).
).
Так як мішаний добуток векторів, серед яких є рівні дорівнює нулю, то в отриманій сумі відмінними від нуля є члени (

 )=(
)=(

 ), що повторюється двічі. Отже, ((
), що повторюється двічі. Отже, (( +
+  )(
)( +
+  )(
)( +
+  ))=2(
))=2(

 ).
).
Відповідь: ( +
+  )(
)( +
+  )(
)( +
+  )=2(
)=2(

 ).
).
16. Довести, що точки А(-1,2,1), В(-3,1,2), С(3,-2,2), D(3,-4,3) належать одній площині.
Розв`язання. Розглянемо три вектори,початок кожного з яких знаходиться у точці А, а кінець - відповідно в точках В, С, D:
 . Знайдемо їх мішаний добуток:
. Знайдемо їх мішаний добуток:  . Виконується умова компланарності векторів
. Виконується умова компланарності векторів  Отже, точки А, В, С, D належать одній площині.
Отже, точки А, В, С, D належать одній площині.
Дата публикования: 2015-09-18; Прочитано: 560 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
