Действия с матрицами

Основными матричными операциями являются:

1) умножение числа на матрицу;

2) умножение матрицы на число;

3) сложение матриц;

4) умножение матриц.

Определение 1. Чтобы умножить число 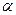на матрицу или матрицу на число 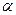, нужно умножить на 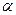все элементы матрицы . Очевидно, .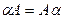

Пример 1.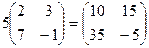

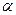Ясно, что для каждой матрицы и каждых чисел и 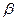имеют место соотношения:

1)

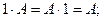
2) ,

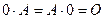3) ; .

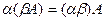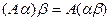Определение 2. Суммой двух матриц 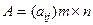и 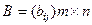одной размерности называется матрица 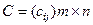той же размерности (обозначается 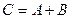), элементы которой определяются равенствами

, .

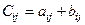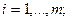
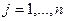Пример 2. Пусть 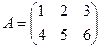, 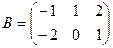. Тогда .

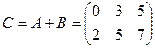Пример3. Пусть 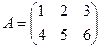, 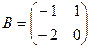. Матрицы и 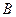сложить нельзя, так как у них разные размерности: у матрицы размерность 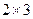, а у матрицы - .

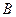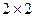Очевидно,

1) 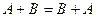(сложение матриц коммутативно);

2) 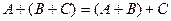(сложение матриц ассоциативно);

3)

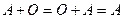
4) , ;

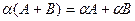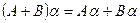5) , .

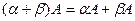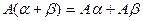Вводя обозначение

,

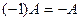будем также иметь

6)

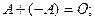
7) ;

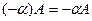8) ;

9) .

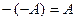Для краткости вместо 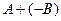пишут .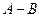

Замечание 1. Поскольку строки и столбцы являются частным случаем матриц, можно говорить о 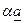, , 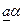, , 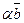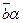а также 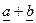или .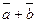

Пример 4. Пусть 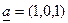, 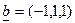. Тогда .

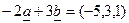В отличие от операций сложения и умножения на число операция умножения

матрицы на матрицу определяется более сложным образом.

Определение3. Пусть заданы две матрицы и 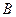, причем число столбцов первой из них равно числу строк второй:

,

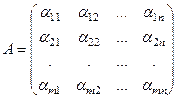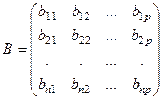
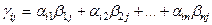
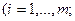
Положим 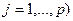. Матрица

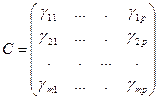
называется произведением на 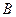и обозначается .

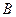Замечание 2. Размерность произведения матриц можно определить по правилу, которое в дальнейшем будет называться правилом умножения размерностей:

.

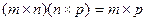Пример5. Пусть , .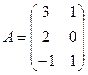

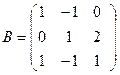Произведение матрицы на матрицу 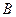не определено, так как число столбцов матрицы не равно числу строк матрицы .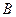

В то же время произведение матрицы 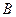на матрицу определено, причем 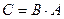имеет размерность 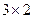. Действительно, используя правило умножения размерностей, имеем

.

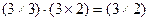Согласно определению произведения матриц

.

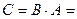
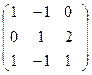
Замечание3. Произведение квадратных матриц определено тогда и только тогда, когда эти матрицы имеют один и тот же порядок 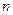. При этом произведение так же будет квадратной матрицей порядка .

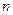Пример6. Пусть 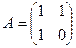и 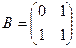. Имеем

,

.

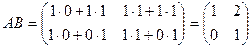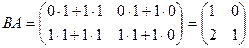Таким образом, мы можем сделать важный вывод: при перемножении матриц нельзя менять порядок сомножителей (произведение матриц не коммутативно).

Свойства операции умножения матриц.

1) Произведение матриц, если оно имеет смысл, ассоциативно, т.е.

;

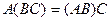2) Произведение матриц дистрибутивно относительно сложения, т.е.

;

;

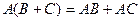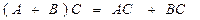3) 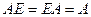для любой квадратной матрицы .