 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дифференциал функции
|
|
Пусть функция дифференцируема на некотором отрезке 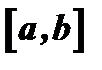 , тогда
, тогда

На основании свойства бесконечно малой можно записать: если  , то
, то 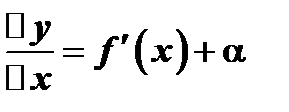 , где
, где 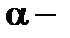 бесконечно малая. Отсюда
бесконечно малая. Отсюда 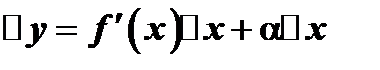 . Таким образом,
. Таким образом, 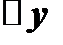 состоит из двух слагаемых, из которых первое слагаемое есть так называемая главная часть приращения, линейная относительно
состоит из двух слагаемых, из которых первое слагаемое есть так называемая главная часть приращения, линейная относительно 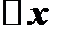 .
.
Произведение производной 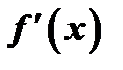 на приращение
на приращение 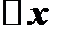 аргумента называется дифференциалом функции и обозначается:
аргумента называется дифференциалом функции и обозначается:

Найдем дифференциал функции 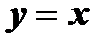 ; в этом случае
; в этом случае 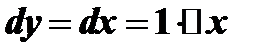 , откуда
, откуда 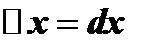 и
и
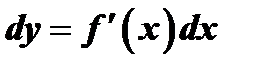
Дифференциал функции обладает следующими свойствами:
1) 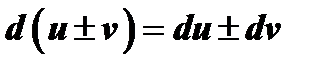 ;
;
2) 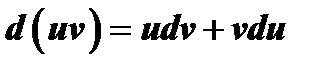 ;
;
3) 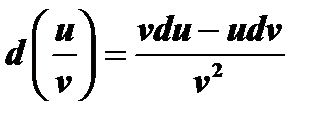
Дата публикования: 2015-09-17; Прочитано: 275 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
