Критерий Рауса –Гурвица

Критерий Рауса — Гурвица является алгебраическим критерием устойчивости. Критерий дает условия, при выполнении которых характеристический многочлен любой степени не содержит корней с положительной вещественной частью.

Критерий Рауса - Гурвица дается в виде неравенств, причем последние записываются в виде определителей, составляемых по особым правилам из коэффициентов характеристического уравнения. Пусть мы имеем характеристическое уравнение системы порядка п.

Приведем это уравнение к виду, при котором аn>0, и составим определитель Гурвица из коэффициентов характеристического уравнения по следующему правилу: по главной диагонали выписываем коэффициенты начиная с α₀ до α_n-1справа от главной диагонали по строкам выписываем коэффициенты по убывающим индексам, слева - по возрастающим. Оставшиеся места заполняем нулями. Итак, определитель Гурвица представлен выражением характеристический многочлен не имеет корней в правой полуплоскости и на мнимой оси, если при αn>0 все п определителей не равны нулю и положительны, т. е. cформулированное условие устойчивости является необходимым и достаточным.

Некоторые частные случаи: Система третьего порядка имеет уравнение

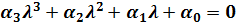(1.25)

и определитель

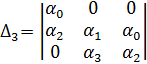
Условия устойчивости:

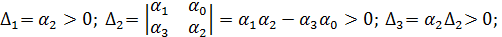
Из последнего неравенства вытекает, что α₀>0, так как ∆₂>0. Из неравенства ∆₂>0 при α₃>0; а₂>0; α₀>0 вытекает, что и α₁>0. Таким образом, система устойчива, если

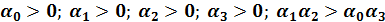(1.26)

Как видно, для уравнения системы третьего порядка недостаточно только положительности коэффициентов уравнения. Необходимо, кроме этого, выполнение неравенства (1.26), т. е. произведение средних коэффициентов должно быть больше произведения крайних.

Положительность коэффициентов уравнения и отличие их от нуля являются необходимым условием устойчивости (для уравнений систем первого и второго порядка необходимое условие является в то же время и достаточным). Поэтому если среди п коэффициентов (от а_п-1 до а₀ включительно) какой-либо коэффициент равен нулю или среди всех п+1 коэффициентов (от а_п до а₀) какой-либо отрицателен, то система неустойчива.

Рассмотрим пример исследования устойчивости с применением критерия Гурвица. Исследуем устойчивость системы стабилизации крена самолета согласно ранее приведенной структурной схеме (рис. 1.39).

характеристическое уравнение замкнутой системы

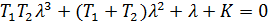
T1T2>0; (T1+T2)>0; K>0- необходимые условия устойчивости выполняются.

Достаточные условия устойчивости:

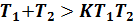(1.27)

Значение коэффициента усиления K, при котором система находится на границе устойчивости, называется критическим коэффициентом усиления.

В нашем примере критический коэффициент усиления будет

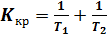(1.28)

При всех К<К_кр система устойчива. Желательно иметь К_кр по возможности большим. Однако это не всегда возможно сделать, так как получить малые значения Т₁ и Т₂ трудно. Существенного увеличения критического коэффициента усиления можно добиться введением дополнительного сигнала по угловой скорости крена от ДУС.