Тема 1. 5. Типовые динамические звенья систем автоматики

Любое автоматическое устройство можно представить в виде простейших составных частей - звеньев, которые обладают динамическими свойствами этого автоматического устройства. Зависимость выходной величины звена от входной (при переходном процессе) определяет динамическая характеристика звена. Конструктивное исполнение, принцип действия и схемы звеньев, входящих в системы автоматического регулирования, могут быть различными. Однако их можно свести к нескольким так называемым типовым звеньям, если в основу классификации положить зависимость входных и выходных величин звена от времени. Эту зависимость называют еще динамической характеристикой. Динамические характери­стики звеньев описываются дифференциальными уравнениями.

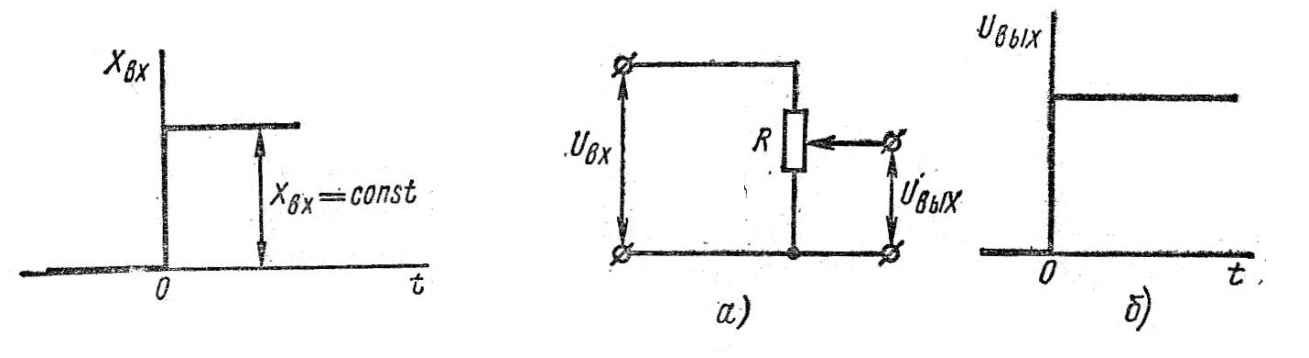
При определении динамических свойств в качестве типовой входной величины принимают скачкообразную функцию (рис. 1.31).При подаче на вход звена величины в виде мгновенного скачка выходная величина во время переходного процесса изменяется по определенному закону.

Рис.1.31. Типовая скачкообразная функция при воздействии на звенья

Рис.1.32. Схема безинерционного звена (а) и его его временная диаграмма (б).

В зависимости от характера протекания переходного процесса различают следующие типовые звенья систем автоматического регулирования: безынерционные, апериодические, дифференцирующие, интегрирующие и колебательные.

Безынерционным называют звено, в котором выходная величина Хвых пропорциональна входной Хвх:

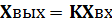(1.2)

где К -коэффициент усиления или передаточное число звена.

Это звено называют также идеальным, усилительным, пропорциональным или безъемкостным. Примерами безъемкостного звена являются делитель напряжения, электронный усилитель, редуктор, рычаг, трансформатор и т. п. При подаче на вход звена скачкообразного сигнала на его выходе сигнал появляется без запаздывания. Поэтому такие звенья и называют безынерционными. Схема безынерционного звена и зависимость его выходной величины от времени показаны на рис.1.32.

Апериодическим называют звено, в котором при скачкообразном изменении -входной величины его выходная величина запаздывает относительно входной и изменяется по экспоненциальному закону с постоянной времени Т. Это звено называют инерционным, статическим, одноемкостным, релаксационным. Примерами апериодического звена служат контуры, состоящие из резистора и конденсатора или из катушки индуктивности и резистора; электродвигатели постоянного тока с независимым возбуждением; двухфазные асинхронные двигатели. Для апериодического звена, схема которого состоит из резистора и конденсатора (рис. 1.33, а), справедливо следующее уравнение:

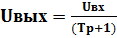(1.3)

где: р- оператор или сокращенная запись операции дифференцирования;

T=RC- постоянная времени.

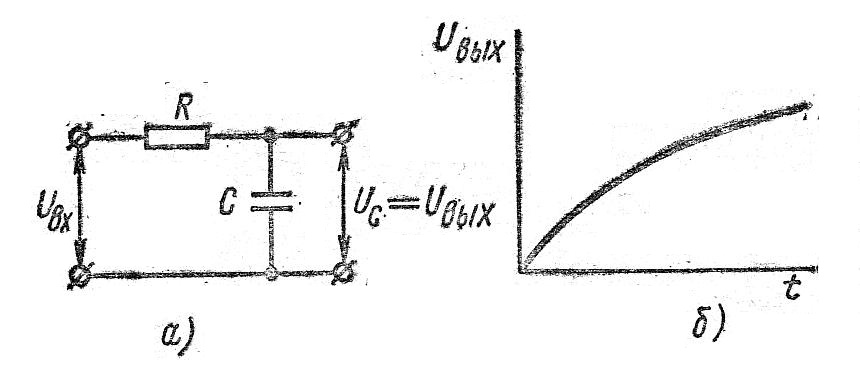
Рис. 1.33. Схема апериодического звена (a) и его временная диаграмма (б)

Решением этого дифференциального уравнения является выражение:

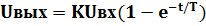(1.4)

На рис. 1.33,б построена зависимость (1.4) от времени, при подаче на вход ступенчатого сигнала.

Дифференцирующим называется звено в котором выходная величина изменяется пропорционально скорости изменения входной величины. Примеры таких цепей- индуктивности и активное сопротивление, емкость и активное сопротивление. На рис.1.34а изображено дифференцирующее звено из конденсатора и резистора.

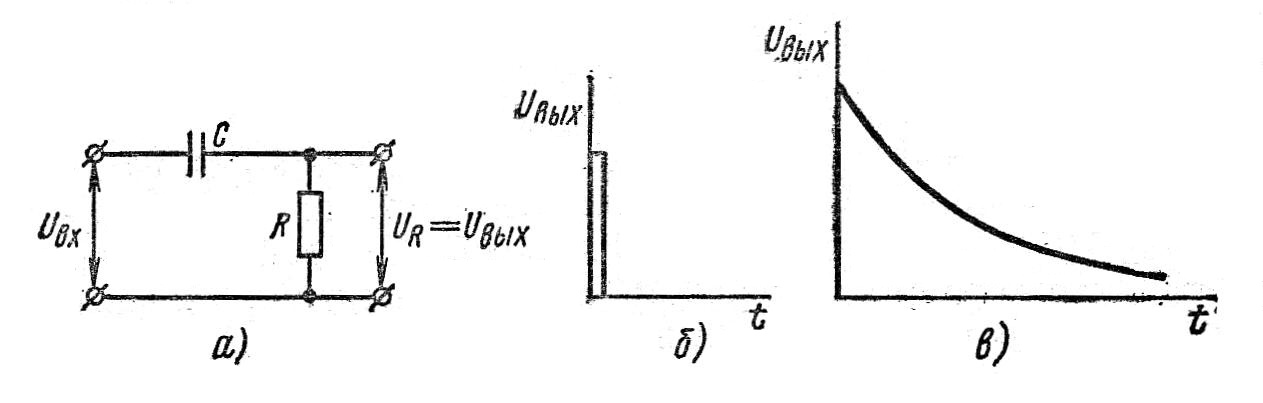
Рис. 1.34. Схема (а) и временные диаграммы дифференцирующего звена: (б) – идеального (в)- реального звена

Для идеального дифференцирующего звена дифференциальное уравнение имеет вид:

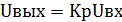(1.5)

Временная характеристика идеального дифференцирующего звена приведена на рис. 1.34, б.

С учетом постоянной времени Т для реального дифференцирующего звена дифференциальное уравнение в операторной форме имеет вид:

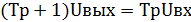(1.6)

Решив это уравнение, получим уравнение динамической характеристики реального дифференцирующего звена:

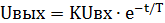(1.7)

Эта характеристика имеет вид убывающей экспоненты (рис. 1.34, в).

Интегрирующим называют звено, в котором выходная величина пропорциональна интегралу по времени от входной величины. Это звено называют астатическим, а также нейтральным. Интегрирующими звеньями считают электродвигатель (выходной величиной является угол поворота вала), конденсатор, дроссель с нулевым активным сопротивлением. На рис. 1.35,а приведена схема интегрирующего звена- электродвигателя постоянного тока с независимым возбуждением. При постоянном напряжение на входе двигателя частота вращения вала двигателя является постоянной величиной. Угол поворота вала φ будет линейно зависеть от времени (рис. 1.35,б)

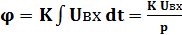(1.8)

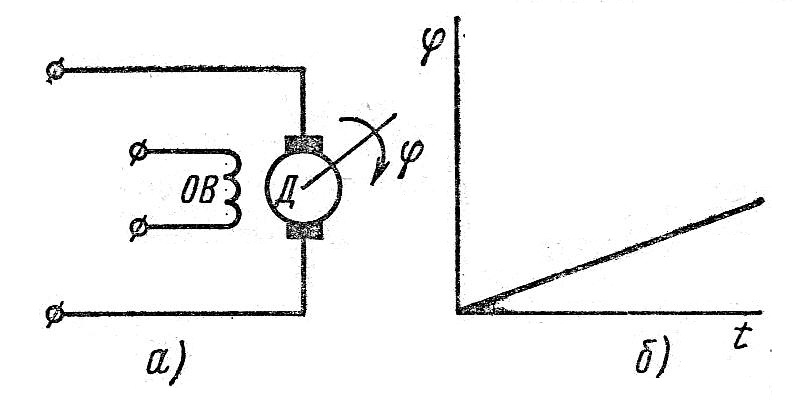
Рис. 1.35. Схема интегрирующего звена (a) и его временная диаграмма (б)

Колебательным называют звено, в котором при скачкообразном изменении входной величины величина на выходе стремится к своему новому установившемуся значению, совершая затухающие колебания. Примерами колебательных звеньев служат электрические колебательные контуры, состоящие из активного резистора, катушки индуктивности и конденсатора; механические колебательные устройства, обладающие массой, упругостью и вязким трением (демпфированием).

На рис. 1.36, а приведена схема электрического колебательного звена.

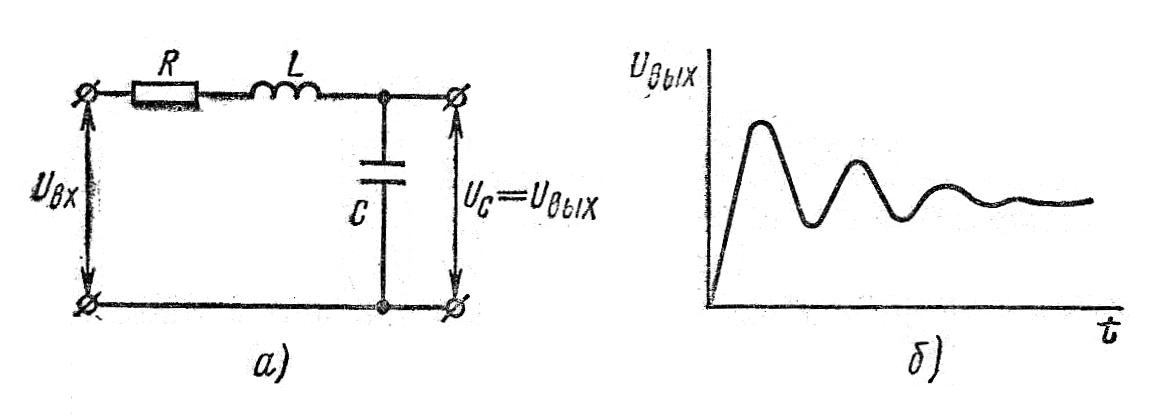
Рис. 1.36. Схема колебательного звена (a) и его временная диаграмма (б)

Для этого звена операторное уравнение:

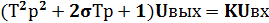(1.8)

где: 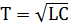- постоянная времени, 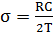-коэффициент затухания

Решение это дифференциального уравнения второго порядка (так как 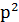), графические представлено на рис.1.36,б (при ступенчатом входном воздействии).

Для анализа свойств звеньев систем автоматического регулирования вводят понятия о передаточных функциях и частотных характеристиках. Передаточной функцией называют отношение мгновенных значений выходной величины к входной. Передаточные функции записываются обычно в операторной форме:

K 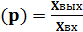(1.9)

Передаточные функции рассмотренных выше типовых звеньев систем автоматического регулирования имею вид:

безинерционное звено

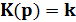(1.10)

апериодическое звено

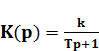(1.11)

идеальное дифференцирующее звено

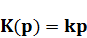(1.12)

реальное дифференцирующее звено

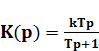(1.13)

интегрирующее звено

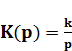(1.14)

колебательное звено

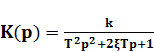(1.15)

Передаточные функции записываются для одного звена, для соединения звеньев, а также для системы в целом.