Тема 1. 6. Устойчивость и качество автоматической системы

Для построения и анализа САР используются три вида схем: функциональная (элементная), принципиальная (электрокинематическая) и структурная (динамическая). С помощью первых двух схем мы изучаем принцип действия систем, определяем состав элементов и устанавливаем функциональную связь между ними. Составление функциональной схемы упрощает задачу составления структурной схемы системы.

Структурной схемой системы называется схема соединения ее элементарных динамических звеньев. Следовательно, для составления структурной схемы системы необходимо предварительно определить передаточные функции ее элементов. Использование структурных схем позволяет существенно упростить методы анализа динамики САР.

Рассмотрим пример составления структурной схемы для системы стабилизации угла крена самолета. Упрощенная принципиальная схема канала крена автопилота АП-28 приведена на рис. 1.37.

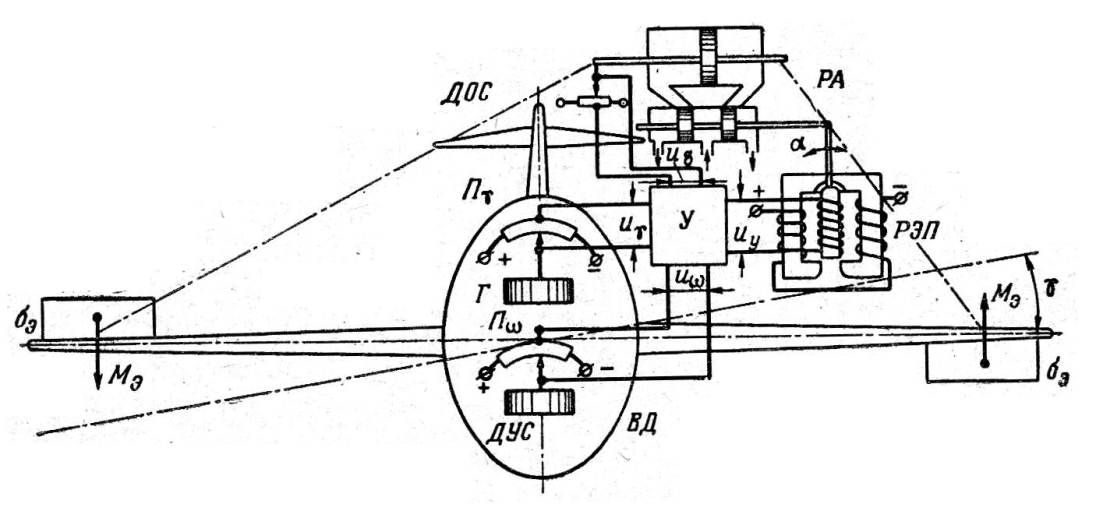
Рис. 1.37. Упрощенная схема системы стабилизации угла крена ВС

Измерителем отклонения угла крена γ самолета от заданного γз является трехстепенной гироскоп Г с потенциометрическом датчиком. Сигнал рассогласования после усиления на электронном усилителе У поступает на пропорциональное электромагнитное реле (РЭП), которое передвигает золотник гидравлического руле­вого агрегата (сервомотора с электрической жесткой обратной связью) РА. Последний управляет положением элеронов. При γ=γз рассогласование ∆γ =0, рулевой привод неподвижен, угол отклонения элеронов δэ =0.

Самолет выдерживает заданное значение угла крена (обычно γ₃ = 0). Если под влиянием возмущений возникает крен самолета и γ не будет равняться заданному, появится отклонение ∆γ=γ-γз которое после усиления заставит сработать пропорционально электромагнитное реле, и рулевой агрегат отклонит элероны на угол δэ, пропорциональный ∆γ. Одновременно перемещается щетка по потенциометру обратной связи ДОС, сигнал с которого поступает на усилитель. При этом на самолет будет действовать момент от элеронов Мэ, который заставляет самолет поворачиваться в сторону уменьшения отклонения. Когда отклонение ликвидируется, система вернется в исходное состояние. Однако в такой системе при отработке возникшего отклонения неизбежны колебания. Это обусловлено инерционностью самолета и других элементов системы. Для улучшения переходных процессов в системе обычно используется сигнал от двухстепенного гироскопа (датчика угловой скорости - ДУС). Он измеряет угловую скорость по крену γ.

Функциональная схема системы приведена на рис. 1.38.

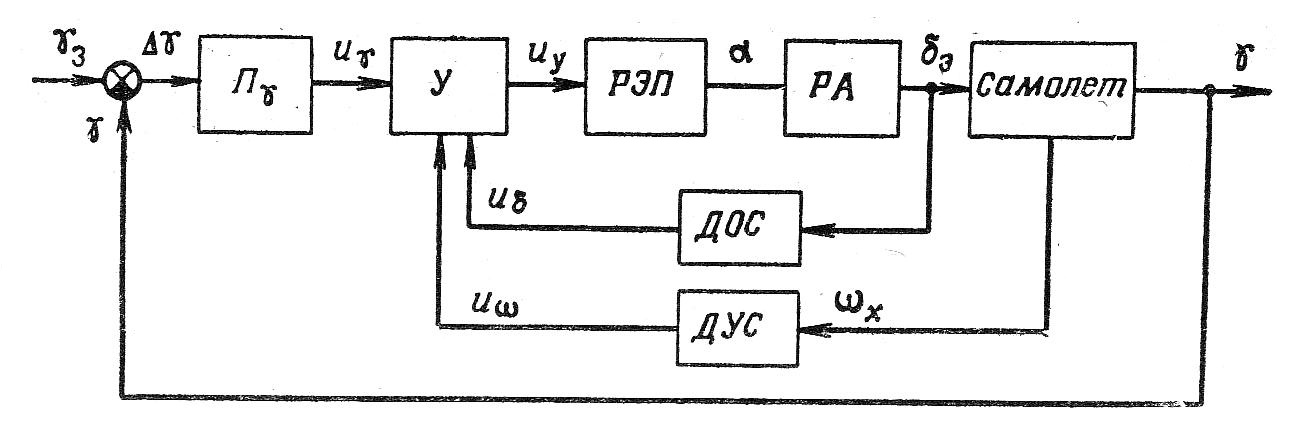
Рис. 1.38. Функциональная схема системы стабилизации угла крена ВС

На схеме указаны основные элементы с их входными и выходными величинами. Для составления структурной схемы запишем уравнения (передаточные функции) элементов системы.

Для измерительного устройства

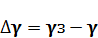(1.16)

Для потенциометрического датчика уравнение имеет вид

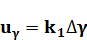(1.17)

где k1 — коэффициент усиления датчика.

Для усилителя уравнение запишется так:

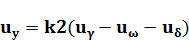(1.18)

где k2— коэффициент усиления.

По динамическим свойствам пропорциональное электромагнитное реле (РЭП) относится к колебательным звеньям. Однако вследствие того что его постоянная времени Tp (около 0,04 с) значительно меньше времени переходного процесса в системе (единицы секунд), Tp обычно не учитывают и приближенно пропор­циональное релепринимают за усилительное звено:

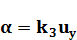(1.19)

где uy— входной сигнал;

α — угол поворота якоря — выходной сигнал;

k3- коэффициент усиления РЭП.

Для рулевого агрегата гидравлический сервомотор имеет передаточную функцию интегрирующего звена:

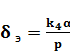(1.20)

где δ_Э — выходная величина; а — входная величина; k4 — коэффициент усиления. '

Для самолета как объекта регулирования передаточную функцию по крену

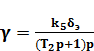(1.21)

Т.е. динамические свойства ВС при вращении аналогичны последовательному соединению инерционного и интегрирующего звеньев.

Уравнение потенциометра обратной связи (ДОС) будет

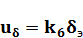(1.22)

Где uδ—напряжение обратной связи;

k6 — коэффициент усиления потенциометрического датчика.

Уравнение датчика угловой скорости (ДУС) имеет вид

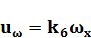(1.23)

где u ω — напряжение, снимаемое с ДУС; k6-коэффициент усиления.

Воспользовавшись полученными передаточными функциями элементов, составим структурную (динамическую) схему системы. Схема системы с отключенным датчиком угловой скорости приведена на рис. 1.39

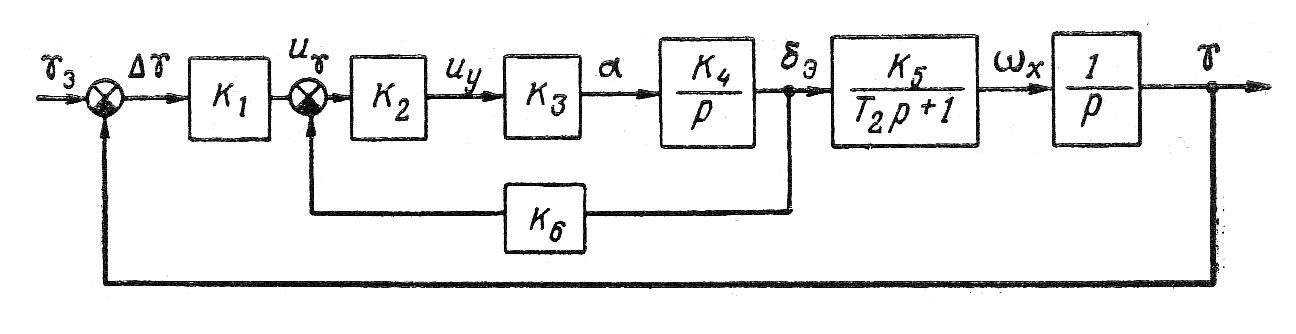
Рис. 1.39. Структурная (динамическая) схема системы стабилизации угла крена ВС при отключенном сигнале ДУС

На рис. 1.40 представлена структурная схема при включенном сигнале ДУС.

Как было сказано ранее отсутствие сигнала ДУС грозит появлению колебаний по крену возле стабилизируемого значения, что нежелательно.

Рис. 1.40. Структурная (динамическая) схема системы стабилизации угла крена ВС при включенном сигнале ДУС

Для исследования динамики системы необходимо определить дифференциальное уравнение или передаточную функцию, связывающую входную γз и выходную γ величины системы. Это уравнение можно получить, исключая из уравнений элементов промежуточные переменные. Однако эта задача проще решается с использованием аппарата структурных схем и методов структурного анализа САР, получившего довольно широкое распространение в последнее время.

Для схемы 1.39 дифференциальное уравнение имеет вид:

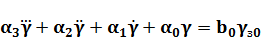(1.24)

Определение понятия устойчивости линейной системы

Устойчивость САР является одной из важнейших характеристик, определяющих ее работоспособность.

Под устойчивым состоянием системы понимается такое состояние, при котором она, будучи выведенной из состояния равновесия каким-либо воздействием, возвращается к первоначальному положению равновесия после устранения этого воз­действия. С точки зрения устойчивости нам не важен характер переходного процесса в системе в процессе перехода в исходное состояние, важно, чтобы этот процесс был затухающим.

Мы будем рассматривать устойчивость только линейных систем, в частности таких систем, динамика которых описывается линейными дифференциальными уравнениями с постоянными коэффициентами. Чтобы судить об устойчивости системы, необходимо найти решение ее дифференциального уравнения и исследовать это решение.

Возьмем для примера уравнение замкнутой системы стабилизации угла крена самолета (1.24) при задающем воздействии типа ступенчатой функции. Решение этого уравнения будет переходной функцией системы, которая в данном случае укажет закон перехода к новому значению угла крена самолета.

Таким образом, знаки вещественных корней и знаки вещественных частей комплексных корней целиком и полностью определяют затухание или незатухание переходной составляющей, т. е. устойчивость или неустойчивость системы.

Линейная система устойчива, если все вещественные корни ее характеристического уравнения отрицательны, а все комплексные имеют отрицательную вещественную часть.

Система, у которой хотя бы один из корней характеристического уравнения положительный или пара комплексных сопряженных корней имеет положительную вещественную часть, является неустойчивой и система непригодна для эксплуатации.

Корням с нулевой действительной частью соответствует критический случай, когда система находится на границе устойчивости. Такая система к эксплуатации непригодна. Таким образом, вопрос устойчивости САР решается на основе анализа знаков корней характеристического уравнения. Если корни известны, вопрос устойчивости системы решен. Однако корни уравнений высоких степеней отыскать трудно, тем более, что для уравнений выше четвертой степени они вообще не выражаются алгебраически (в виде формул) через коэффициенты уравнения. В связи с этим возникла необходимость судить об устойчивости системы непосредственно по коэффициентам характеристического уравнения или по коэффициентам передаточной функции. Эти коэффициенты сравнительно просто выражаются через параметры звеньев, образующих системы.

Для того чтобы при исследовании устойчивости системы обойти операцию определения корней характеристического уравнения, были разработаны и предложены так называемые критерии устойчивости.

Критерии устойчивости -это правила, согласно которым можно судить об устойчивости, минуя операцию определения корней. Использование критериев устойчивости дает возможность относительно просто установить причину неустойчивости системы.

Существуют алгебраические и частотные критерии устойчивости, эквивалентные с математической точки зрения друг другу.