Теоретические сведения. Задачей корреляционною анализа является выявление линейной связи между случайными величинами и определение формы связи между ними

Задачей корреляционною анализа является выявление линейной связи между случайными величинами и определение формы связи между ними, надежности и доверительных границ параметров уравнений регрессии.

Для системы двух случайных величин Х и У характеристиками являются начальные моменты М(Х), М(У), центральные моменты D(X), D(y), корреляционный момент k_xy, коэффициент линейной корреляции . В статистике используются их выборочные оценки.

Если объем выборки невелик, выборочные моменты определяются по следующим формулам:

• выборочные средние ,
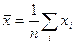• исправленные выборочные дисперсии

• выборочный корреляционный момент

(1)

• выборочный коэффициент линейной корреляции

(2)

При большом объеме выборки составляется корреляционная таблица, в которой показаны частоты m появления каждой пары значений признаков (х; y). В этом случае выборочные моменты вычисляются по формулам:

• выборочные средние , (3)
• выборочные дисперсии

(4)

• корреляционный момент

(5)

• выборочный коэффициент корреляции (6)

Оценка значимости коэффициента корреляции выполняется с помощью случайной величины , распределение которой подчиняется закону Стьюдента в предположении, что система (х, y) распределена нормально. Вычислив эмпирическое значение этого критерия

, (7)

по таблице t -распределения Стьюдента необходимо найти его критическое значение t = t_кр. Интервальная оценка для генерального коэффициента корреляции ρ_xy имеет вид

, (8)

где .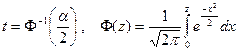

Задачей регрессионного анализа является определение формы и параметров уравнений регрессии, характеризующих зависимость между случайными признаками, а также оценка значимости и доверительных границ этих параметров.

При малом объеме выборки система случайных величин (Х,Y) задается небольшим количеством пар чисел (х_i, у_i), i =1,2,..., n. В координатной плоскости хОy эти точки образуют некоторую ломаную, и если она может быть аппроксимирована прямой, то параметры ее уравнения находят методом наименьших квадратов. В итоге выборочное уравнение прямой регрессии приобретает вид

. (9)

При большом объеме выборки, когда система случайных величин задана корреляционной таблицей, прямые регрессии Y на Х и Х на Y различны, они пересекаются в точке 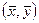и их выборочные уравнения имеют вид

, (10)