Теоретические сведения. Статистической проверкой гипотез называется проверка предположений о законах распределения изучаемого признака

Статистической проверкой гипотез называется проверка предположений о законах распределения изучаемого признака, об однородности выборок, о значениях пара метров генеральной совокупности и т. д.

Пусть имеется выборка х₁,х₂, …,х_n из генеральной совокупности, распределение которой характеризуется некоторым параметром. Пусть относительно этого параметра высказывается некоторое предположение. Назовем его нулевой гипотезой и обозначим Но. Предположение, противоречащее гипотезе Но, называют альтернативной (конкурирующей) гипотезой и обозначают Н ₁.

Ввиду того, что выборка всегда несет в себе элемент случайности, статистически подтвержденную гипотезу следует расценивать не как абсолютно верный факт, а лишь как достаточно правдоподобное утверждение, не противоречащее данному опыту. Может оказаться, что некоторая выборка заставит нас отвергнуть заведомо верную гипотезу, или наоборот. Такие ошибки называются ошибками I и II рода.

Проверка нулевой гипотезы осуществляется с помощью количественного критерия – функции результатов наблюдений θ(х₁,х₂, …,х_n). Будучи случайной величиной, θ(х₁,х₂, …,х_n) подчинена одному из законов, зависящих только от объема выборки п (в предположении справедливости гипотезы Но). Основными из них являются известные законы: χ ² -распределение, t - распределение Стьюдента и F -распределение Фишера.

Все множество возможных значений случайной величины θ можно разбить на два непересекающихся подмножества: Ω – область допустимых значений критерия и W – критическую область. Вероятность попадания критерия в область W обозначается β и называется уровнем значимости, а вероятность α попадания в область Ω – уровнем достоверности (надежности).

Решающим правилом для принятия нулевой гипотезы является попадание эмпирического значения критерия θ_эмп в область допустимых значений Ω. Если θ_эмп оказалось в критической области W,:гипотеза отвергается.

Критическими точками (границами) θ_кр называются границы областей Ω и W. Правосторонней называется критическая область, определяемая неравенством θ > θ_кр; левосторонней называется критическая область, определяемая неравенством θ < θ_кр. Двусторонней называется критическая область, определяемая неравенствами θ₂ < θ < θ₁, где θ₁ > θ₂. В частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенством |θ| > θ_кр.

Пусть имеются две независимые выборки малого объема п ₁ и п ₂ из двух нормальных генеральных совокупностей, по которым вычислены выборочные средние 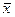и и исправленные выборочные дисперсии и . Необходимо проверить нулевые гипотезы о равенстве генеральных средних (т_х = т_у) и генеральных дисперсий , когда различие выборочных средних и дисперсий несущественно. Такие гипотезы о равенстве параметров распределений называются простыми.

Гипотеза о равенстве гeнеральных средних может быть проверена лишь при условии, что генеральные дисперсии обоих признаков равны. Поэтому сначала проверяется нулевая гипотеза Но о равенстве дисперсий. Эта задача сводится к сравнению выборочных дисперсий и (при альтернативной гипотезе ). Для построения критической области с заданным уровнем значимости β используется F -распределение Фишера, плотность которого зависит только от объемов выборок п ₁ и п ₂.

Эмпирическое значение критерия определяется как отношение выборочных дисперсий

или (1)

(отношение составляется так, чтобы оно было больше единицы).

Критическое значение F_кр определяют по таблице F -распределения Фишера при уровне значимости β и степенях свободы ν ₁ = n ₁–1 и ν ₂ = n ₂–1.

Если F_эмп ≤ F_кр, то гипотеза Но принимается, если F_эмп > F_кр, то гипотеза отвергается.

В случае, если гипотеза о равeнствe дисперсий подтверждена, приступают к проверке гипотезы о равенстве генеральных средних. В качестве их точечных оценок т_х и т_у используют выборочные средние 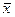и , а в качестве единой оценки дисперсии – средневзвешенную дисперсию

. (2)

Если гипотеза Но о средних верна, то случайная величина распределена нормально с математическим ожиданием т_z = 0 и дисперсией . Тогда случайная величина подчинена t -распределению Стьюдента с ν = n ₁+ n ₂ – 2 степенями свободы и служит критерием для оценки гипотезы о равенстве т_х = т_у.

Критическое значение t_кр, соответствующее числу степеней свободы ν = n ₁+ n ₂ – 2 и заданному уровню значимости β, определяют по таблице t -распределения Стьюдента.

При альтернативной гипотезе т_х ¹ т_у, эмпирическое значение t_эмп находят по формуле

, (3)

где , а величина определяется формулой (2).

Если | t_эмп | ≤ t_кр, то с надежностью α=1– β гипотеза считается справедливой, в противном случае гипотеза отвергается.