Властивості афінних перетворень

Проаналізуємо основні властивості афінних перетворень. При цьому будемо вважати, що афінне перетворення задається відповідністю реперів 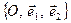та .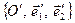

1. Вектор при афінному перетворенні переходить у вектор з такими ж координатами.

2. При афінному перетворенні колінеарні вектори відображаються у колінеарні.

Доведення даних тверджень очевидне, оскільки пари відповідних точок 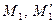та мають однакові координати.

3. При афінному перетворенні пряма переходить у пряму, а паралельні прямі – у паралельні.

Доведення. Нехай задано деяку пряму, яка у системі координат задається рівнянням 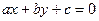, . Координати образів кожної точки прямої, які є такими ж, теж задовольнятимуть дану рівність, тому точки фігури, яка є образом даної прямої, утворюють пряму. Дві паралельні прямі, задані рівняннями та перейдуть у прямі, які задаються такими ж рівняннями, тобто у паралельні прямі.

4. При афінному перетворенні відрізок переходить у відрізок, причому точка, яка ділить відрізок, який ми відображаємо, у деякому відношенні, переходить у точку, яка ділить образ відрізка у тому ж відношенні.

Доведення. Нехай точки та , які є кінцями відрізка , при афінному перетворенні переходять у точки та і точка 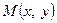, яка ділить відрізок у відношенні , переходить у точку . Тоді для координат точки виконуються рівності

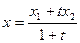, , (7)

які будуть виконуватись і для образів взятих точок, оскільки вони мають такі самі координати. При дістаємо, що внутрішні точки відрізка переходять у внутрішні точки відрізка , а із того, що співвідношення (7) виконуються для точок , та випливає, що точка ділить відрізок у такому ж відношенні . Зокрема, при афінному перетворенні середина відрізка переходить у середину відрізка.

5. При афінному перетворенні півплощина перетворюється у півплощину.

Доведення. Нехай півплощина обмежена прямою, яка задається рівнянням 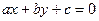. Тоді півплощина задається однією із нерівностей або . При афінному перетворенні точки півплощини перейдуть у точки нової фігури, координати яких, будучи рівними координатам прообразів, теж задовольнятимуть одну із даних нерівностей. Тому образом півплощини є півплощина.

6. Існує єдине афінне перетворення, яке одну трійку не колінеарних точок (тобто точок, які не лежать на одній прямій) переводить в іншу.

Доведення. Будемо шукати афінне перетворення, яке три довільні не колінеарні точки переводить у три не колінеарні точки . Підставляючи координати точок у рівності (1), дістаємо систему лінійних рівнянь

, ,

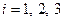де невідомими є коефіцієнти та . Обчислимо визначник , складений із коефіцієнтів біля невідомих.

,

оскільки точки не лежать на одній прямій. Отже, система має єдиний (ненульовий) розв’язок. Умова не колінеарності точок 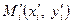випливає з вимоги невиродженості матриці 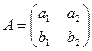. Справді, якби точки 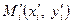були колінеарними, то не існувало б оберненого перетворення, оскільки замінюючи точки на точки 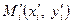, ми отримали б аналогічний визначник , який рівний нулю.

Для того, щоб задати перетворення, яке три не колінеарні точки переводить у три не колінеарні, достатньо побудувати дві афінні системи координат та , де 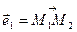, , , . Афінне перетворення, яке визначається цими двома системами координат, переводить точки та відповідно у точки та , є шуканим.