Афінна еквівалентність фігур

Назвемо фігуру афінно еквівалентною фігурі 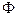, якщо у групі афінних перетворень знайдеться перетворення, яке фігуру 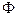переводить у фігуру .

Відношення афінної еквівалентності має властивості рефлективності, симетричності та транзитивності. Це означає, що:

1) кожна фігура афінно еквівалентна сама собі (вона переводиться в себе тотожнім перетворенням);

2) якщо фігура 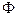афінно еквівалентна фігурі то фігура афінно еквівалентна фігурі 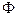, оскільки вона переводиться в неї оберненим перетворенням;

3) якщо фігура 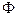афінно еквівалентна фігурі , а фігура - фігурі , то фігура 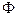афінно еквівалентна фігурі , оскільки вона переводиться в неї перетворенням, яке є композицією двох перетворень, перше з яких переводить 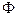у , а друге - у .

Наведемо приклади афінно еквівалентних фігур.

1). Два довільні трикутники афінно еквівалентні.

Доведення даного твердження випливає із властивості 6.

2). Два опуклих чотирикутники будуть афінно еквівалентними, якщо точка перетину ділить їхні діагоналі в одному і тому ж відношенні.

Справді, нехай у чотирикутнику діагоналі і перетинаються у точці 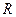, а діагоналі та чотирикутника - у точці (рис. 1), причому та .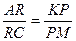

Нам відомо, що трикутники та афінно еквівалентні. Афінне перетворення, яке переводить репер у репер 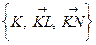, відображає точку 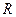у точку , оскільки .

Враховуючи те, що точки 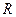та за умовою відповідно ділять відрізки та в однаковому відношенні, розглянуте афінне перетворення переводить точку 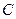у точку , а, отже, чотирикутник - у чотирикутник .

Дослідимо питання афінної еквівалентності ліній другого порядку.

Теорема. Два довільні еліпси, дві гіперболи та дві довільні параболи афінно еквівалентні.

Доведення. Розглянемо два еліпси, задані рівняннями та . Очевидно, що афінне перетворення, яке задається рівностями

,

переводить перший із них у другий, тому вони афінно еквівалентні. Аналогічно виконується доведення у випадку гіпербол.

Нехай задані дві параболи та . Легко перевірити, що перетворення, визначене рівностями

,

є афінним та переводить першу параболу у другу. Тому дві довільні параболи афінно еквівалентні.

Будь-який уявний еліпс, який задається рівнянням , перетворенням

переводиться в уявне коло , тому два уявні еліпси, будучи афінно еквівалентними уявному колу, є афінно еквівалентними.

Дві прямі, які перетинаються, як ми знаємо, можна задати рівнянням , де . Перетворення, задане рівностями

,

є афінним, оскільки . Воно переводить дані прямі у фігуру, задану рівнянням , тобто у дві прямі та , які перетинаються і є осями координат нової афінної системи. Аналогічно, дві паралельні прямі, які можна задати рівнянням афінним перетворенням

,

переводяться у дві паралельні прямі, рівняння яких легко одержати з рівності . Якщо , то можна взяти перетворення, яке задається системою

.

Дві прямі, які співпадають, можна задати рівнянням 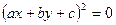. Перетворення

,

переводить їх у дві прямі, які співпадають та задаються рівнянням . При можна взяти перетворення, яке задається рівностями

.

Дві уявні прямі, які перетинаються у дійсній точці, або дві уявні паралельні прямі можна задати відповідно рівняннями та . Перетворення

та

переводять їх відповідно у дві уявні прямі , які перетинаються у дійсній точці, та у дві уявні паралельні прямі .

Таким чином, існує 9 класів афінно еквівалентних ліній другого порядку: еліпси (дійсні та уявні), гіперболи, параболи, дійсні прямі, які перетинаються, паралельні або співпадають та уявні прямі, які перетинаються у дійсній точці або паралельні.

Наведемо приклади задач, які показують, як за допомогою афінних перетворень можна встановити вид лінії другого порядку. Метод, яким ми будемо користуватися, називають методом виділення повних квадратів.

Приклад 1. Встановити вид лінії, заданої рівнянням

.

Розв’язання. Перетворимо задане рівняння до виду або . Одержане співвідношення запишемо у виді . Введемо заміну

.

Оскільки , то записані рівності визначають афінне перетворення, яке лінію, задану початковим рівнянням, переводить в афінно еквівалентну лінію, рівняння якої має вид . Очевидно, що дана лінія – гіпербола.

Приклад 2. Яку лінію задає рівняння ?

Розв’язання. Запишемо рівняння у вигляді або та введемо заміну .

Визначник цього відображення відмінний від нуля, отже, воно є афінним перетворенням. Перетворене рівняння набуває виду і, очевидно, визначає параболу.