Метод Гаусса решения линейных систем

Метод Гаусса для невырожденных квадратных линейных систем (3.1) состоит в том, что

1) с помощью элементарных преобразований:

а) перестановки любых двух уравнений местами;

б) прибавление к любому уравнению другого уравнения, умноженного на число

система приводится к равносильной системе

(3.4)

с треугольной основной матрицей, имеющей тот же определитель, что и матрица 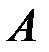, а потому с ненулевыми диагональными элементами , , …, (прямой ход метода);

2) из системы (3.4) последовательно находятся значения неизвестных, начиная с последнего (обратный ход метода):

,…, , .

Заметим, что невырожденность квадратной линейной системы, то есть условие , до начала решения проверять не нужно; если система приводится к виду (3.4), то она невырожденная.

Метод Гаусса можно распространить на любую линейную систему (3.1), добавив к числу элементарных преобразований

в) перенумерацию неизвестных;

г) удаление «нулевого уравнения» 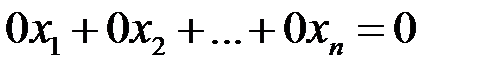, которому удовлетворяет любой набор чисел .

Если по ходу преобразований встретится уравнение вида , где , то оно не имеет решений и, тем более, вся система не имеет решений – несовместна.

Если такое уравнение не встретилось, то система преобразуется в равносильную систему из уравнений

(3.5)

где все те же неизвестные , но возможно пронумерованные в другом порядке, а числа , ,…, не равны нулю.

Если , то, как и выше, обратным ходом получаем единственное решение. Система определенна.

Если , то неизвестным придаем произвольные значения и из (3.5) обратным ходом выражаем последовательно через . В итоге имеем бесконечное множество решений, зависящих от произвольных постоянных , меняя которые получим все решения. Таким образом, в этом случае система неопределенна.