 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Задачи для самостоятельного решения. В задачах 2.1.1-2.1.2. найти матрицы и . 2.3.1
|
|
В задачах 2.1.1-2.1.2. найти матрицы  и
и  .
.
2.3.1.  , ,  . .
| 2.3.2.  , ,  . .
|
В задачах 2.3.3-2.3.4 найти  и
и  .
.
2.3.3. 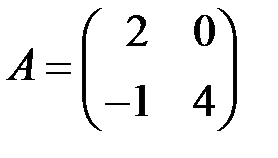 , ,  . .
| 2.3.4.  , ,  . .
|
В задачах 2.3.5-2.3.6 найти  и
и  .
.
2.3.5. 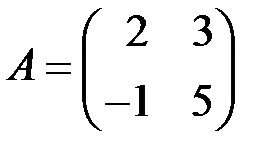 , ,  . .
| 2.3.6. 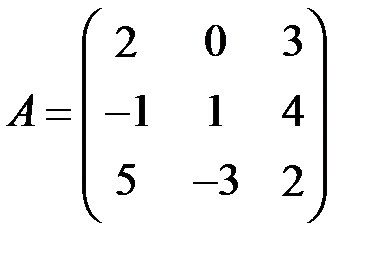 , ,  . .
|
2.3.7. Найти  и
и  , если
, если  ,
,  .
.
2.3.8. Найти  , если
, если  ,
,  .
.
2.3.9. Для матрицы  найти
найти  и
и  .
.
2.3.10. Для матрицы  найти
найти  и
и 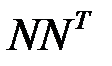 .
.
2.3.11. Для матриц  и
и  найти
найти  ,
,  , …,
, …,  и
и  ,
, 
2.3.12. Для матрицы  найти
найти  ,
, 
2.3.13. Известно, что  , где
, где  –
–  -матрица, а
-матрица, а  –
–  -матрица. Найти размеры матрицы
-матрица. Найти размеры матрицы  .
.
2.3.14. Известно, что  , где
, где  –
–  -матрица, а
-матрица, а  –
–  -матрица, а
-матрица, а  –
–  -матрица. Найти
-матрица. Найти  ,
,  и
и 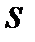 .
.
2.3.15. Пусть  ,
,  и
и  . Существуют ли следующие произведения:
. Существуют ли следующие произведения:
a) 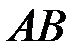 , ,
| b)  , ,
| c)  , ,
| d)  , ,
| e)  , ,
| f)  . .
|
2.3.16. Даны матрицы  ,
,  и
и 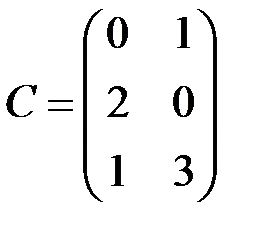 и
и  . Существуют ли следующие произведения:
. Существуют ли следующие произведения:
a) 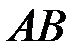 , ,
| b)  , ,
| c)  , ,
|
d)  , ,
| e)  , ,
| f)  , ,
|
g) 
| h)  , ,
| i)  . .
|
В задачах 2.3.17-2.3.18 для матрицы  найти обратную матрицу
найти обратную матрицу  .
.
2.3.17.  . .
| 2.3.18.  . .
|
В задачах 2.3.19-2.2.20 выяснить является ли матрица  обратимой.
обратимой.
2.3.19.  . .
| 2.3.20.  . .
|
В задачах 2.3.21-2.2.22 найти матрицу, обратную к заданной.
2.3.21.  . .
| 2.3.22. 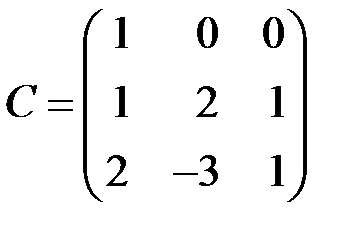 . .
|
2.3.23. Решить матричное уравнение  , где
, где  ,
,  .
.
2.3.24. Решить матричное уравнение  , где
, где  ,
,  .
.
2.3.25. Упростить выражение  , где
, где  и
и  – квадратные матрицы одного порядка.
– квадратные матрицы одного порядка.
2.3.26. Пусть  – квадратная матрица с ненулевым определителем.
– квадратная матрица с ненулевым определителем.
1) Упростить выражение для матрицы  ;
;
2) доказать, что  .
.
2.3.27. Пусть  – квадратная матрица второго порядка с ненулевым определителем. Найти
– квадратная матрица второго порядка с ненулевым определителем. Найти  .
.
2.3.28. Пусть  – квадратная матрица третьего порядка с
– квадратная матрица третьего порядка с  . Найти
. Найти  .
.
Дата публикования: 2015-09-17; Прочитано: 310 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
