 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение систем дифференциальных уравнений операционным методом
|
|
п.1. Определение и основные свойства преобразования Лапласа
Функцией-оригиналом называется комплекснозначная функция  действительного переменного
действительного переменного 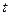 , удовлет-воряющая следующим условиям:
, удовлет-воряющая следующим условиям:
1°  при
при 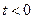 ;
;
2° с возрастанием 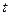 модуль функции
модуль функции  растет не быстрее некоторой показательной функции, т.е. существуют числа
растет не быстрее некоторой показательной функции, т.е. существуют числа  и
и  такие, что для всех
такие, что для всех 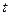 имеем
имеем  ;
;
3° на любом конечном отрезке [a,b] положительной полуоси функция  удовлетворяет условиям Дирихле, т.е.:
удовлетворяет условиям Дирихле, т.е.:
a) она ограничена;
б) либо непрерывна, либо имеет лишь конечное число точек разрыва 1-го рода;
в) имеет конечное число экстремумов.
Изображением функции-оригинала по Лапласу называется функция  комплексного переменного
комплексного переменного  , определяемая равенством
, определяемая равенством
 (1)
(1)
при  . Условие 2 обеспечивает существование интеграла (1).
. Условие 2 обеспечивает существование интеграла (1).
Преобразование (1), относящее оригиналу  его изображение
его изображение  , называется преобразованием Лапласа.
, называется преобразованием Лапласа.
Тот факт, что функция  является изображением оригинала
является изображением оригинала  , обозначается следующими символами:
, обозначается следующими символами:
 или
или  .
.
Уславливаются за значение оригинала  во всякой его точке разрыва 1-го рода
во всякой его точке разрыва 1-го рода  принимать полусумму его предельных значений слева и справа от этой точки:
принимать полусумму его предельных значений слева и справа от этой точки:
 при
при  ;
;
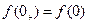 при
при  .
.
При соблюдении этого условия соответствие между оригиналами и изображениями взаимнооднозначно (т.е. всякому оригиналу соответствует единственное изображение и обратно).
Свойства преобразования Лапласа:
Всюду ниже считаем:  и
и  .
.
I. Свойство линейности. Для любых комплексных постоянных  и
и 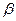
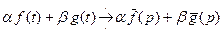 .
.
II. Теорема подобия. Для любого постоянного 
 .
.
III. Дифференцирование оригинала. Если  есть оригинал, то
есть оригинал, то  .
.
Обобщение. Если  n раз непрерывно дифферен-цируема на
n раз непрерывно дифферен-цируема на 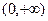 и
и  есть оригинал, то
есть оригинал, то
 .
.
IV. Дифференцирование изображения равносильно умножению оригинала на “минус аргумент”, т.е.
 .
.
Обобщение:  .
.
V. Интегрирование оригинала сводится к делению изображения на  :
:
 .
.
VI. Интегрирование изображения равносильно делению на 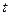 оригинала:
оригинала:

(предполагаем, что интеграл  сходится).
сходится).
VII. Теорема запаздывания. Для любого положительного числа 
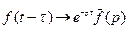 .
.
VIII. Теорема смещения (умножение оригинала на показательную функцию). Для любого комплексного числа 
 .
.
IX. Теорема умножения (Э. Борель). Произведение двух изображений  и
и  также является изображением, причем
также является изображением, причем
 . (2)
. (2)
Интеграл в правой части (2) называется сверткой функций  и
и 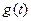 и обозначается символом
и обозначается символом
 .
.
Теорема IX утверждает, что умножение изображений равносильно свертыванию оригиналов, т.е.
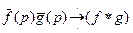 .
.
Таблица 1. Изображения основных элементарных функций
| N | 
| 
| N | 
| 
|

| 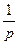
|

| 
| ||
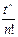
| 
|

| 
| ||

| 
|

| 
| ||

| 
|
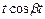
| 
| ||

| 
|

| 
|
В таблице и в каждом из приведенных ниже примеров указывается только значение  при
при  (всегда имеется в виду, что
(всегда имеется в виду, что  , если
, если 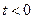 ).
).
п. 2. Отыскание оригинала по изображению
При отыскании оригинала по изображению в простейших случаях используют таблицу изображений основных элементарных функций и теоремы разложения (первую и вторую).
Вторая теорема разложения позволяет найти оригинал для изображения, являющегося дробно-рациональной функцией от  , т.е.
, т.е.  , где
, где 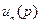 и
и  - многочлены от
- многочлены от  соответственно степени
соответственно степени 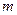 и
и  , причем
, причем  . Если разложение
. Если разложение  (p) на простейшие множители имеет вид
(p) на простейшие множители имеет вид
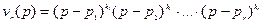 ),
),
где  , то, как известно, функцию
, то, как известно, функцию  можно разложить на сумму элементарных дробей вида
можно разложить на сумму элементарных дробей вида  , где
, где  принимает все значения от 1 до
принимает все значения от 1 до  , а
, а  - все значения от 1 до
- все значения от 1 до  . Таким образом,
. Таким образом,
 (1)
(1)
Все коэффициенты этого разложения можно определить по формуле
 (2)
(2)
Вместо этой формулы для определения коэффициентов  могут быть использованы элементарные приемы, применяемые в интегральном исчислении при интегрировании рациональных дробей. В частности, это целесообразно делать в тех случаях, когда все комплексные корни знаменателя
могут быть использованы элементарные приемы, применяемые в интегральном исчислении при интегрировании рациональных дробей. В частности, это целесообразно делать в тех случаях, когда все комплексные корни знаменателя  простые и попарно сопряженные.
простые и попарно сопряженные.
Если все корни  простые, т.е.
простые, т.е.
 при
при  ),
),
то разложение упрощается:

где
 (3)
(3)
При отыскании тем или иным способом разложения  на простейшие дроби оригинал
на простейшие дроби оригинал  находится по следующим формулам:
находится по следующим формулам:
а) в случае кратных корней знаменателя  :
:
 (4)
(4)
б) в случае простых корней знаменателя  :
:
 (5)
(5)
Если изображение искомой функции может быть разложено в степенной ряд по степеням 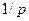 , т.е.
, т.е.

(причем этот ряд сходится к  при
при  , где
, где
 ), то оригинал
), то оригинал  находится по формуле
находится по формуле

причем этот ряд сходится для всех значений 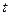 (первая теорема разложения).
(первая теорема разложения).
п. 3. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами
Пусть требуется найти решение системы двух уравнений с постоянными коэффициентами
 (1)
(1)
удовлетворяющее начальным условиям
 (2)
(2)
Будем предполагать, что функции 
 , а также
, а также  и
и  являются функциями-оригиналами. Пусть
являются функциями-оригиналами. Пусть

По правилу дифференцирования оригиналов (см. свойство III п.2), с учетом (2), имеем:
 .
.
Применяя к обеим частям каждого из уравнений системы (1) преобразование Лапласа, получаем операторную систему:

Эта система является линейной алгебраической системой двух уравнений с двумя неизвестными  и
и  . Решая ее, мы найдем
. Решая ее, мы найдем  и
и  , а затем, переходя к оригиналам, получим решение
, а затем, переходя к оригиналам, получим решение  системы (1), удовлетворяющее начальным условиям (2).
системы (1), удовлетворяющее начальным условиям (2).
Аналогично решаются линейные системы вида

Дата публикования: 2015-09-17; Прочитано: 860 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
