Неопределённые уравнения второго порядка

Два вида таких уравнений были рассмотрены до Диофанта. Это уравнения x² + y² = z² и x² – ay² = 1. Первое из них появилось ещё в Древнем Вавилоне. Формулы для его решения были найдены пифагорейцами:

x = k² – 1, y = 2k, z = k² + 1.

Второе полностью решается в «Началах» Евклида для случая a=2, причём не в рациональных, а в целых числах. Решение его для произвольного неквадратного a, вероятно, знал Архимед, поставивший перед Эратосфеном известную «Задачу о быках».

Диофант в книге II своей «Арифметики» рассматривает различные неопределённые уравнения второго порядка и устанавливает, по существу, следующую теорему: неопределённое уравнение второго порядка от двух переменных либо не имеет ни одного рационального решения, либо имеет их бесконечно много, причём в последнем случае все решения выражаются как рациональные функции параметра

x = φ(k), y = ψ(k), где φ и ψ — рациональные функции. Чтобы показать это, приведём сначала задачу 8 книги II.

«Данный квадрат разделить на два квадрата. Пусть предложено 16 разделить на два квадрата. И положим первый x2, а другой тогда будет 16 – x2; таким образом, должно быть 16 – x2 = . Образуем этот квадрат из нескольких x минус столько единиц, сколько содержится в стороне 16; пусть будет 2x – 4, что в квадрате даст 4x2 + 16 – 16x. Это равно 16 – x2. К обеим частям прибавим отрицательные (члены) и сделаем приведение подобных. Тогда 5x2 = 16x и x = 16/5. Один будет 256/25, другой 144/25, сумма их будет 400/25 = 16, и каждый из них будет квадратом».

Попробуем теперь выделить метод Диофанта «в чистом виде». Итак, пусть дано уравнение

x2 + y2 = a2,

(6)

которое представляет окружность с центром в начале координат. Одним из рациональных решений этого уравнения будет (0, –a). Диофант делает подстановку:

x = x, y = kx – a.

(7)

Не имея обозначений для произвольного k, он берёт k=2, отмечая, однако, что следует образовать квадрат из «нескольких x минус столько единиц, сколько содержится в стороне 16», т.е. в нашей символике это в точности kx–4.

Подстановку (7) можно интерпретировать геометрически как проведение через точку (0, –a) прямой

y = kx – a.

Эта прямая встретит окружность (6) ещё в одной точке, координаты которой будут рациональными функциями от k. Действительно,

x² + (kx – a)² = a²

и

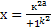, y = kx – a = a,

О числе

Значение π=З при измерении круга нередко применялось в обиходе землемеров и в учебниках математики многие столетия после «Математики». Вероятно, это значение было получено сначала отдельно для длины окружности и для площади круга, без осознания связи между обеими величинами. Быть может, совпадение значений π в обоих случаях явилось сперва результатом эмпирических или полуэмпирических измерений; например, круг принимали равновеликим 3/4 описанного квадрата, а окружность — равной периметру правильного вписанного шестиугольника. Составителям «Математики» в девяти книгах» зависимость между длиной окружности и площадью круга была уже известна. Но они же при вычислении объема шара пользовались правилом, соответствующим другому значению π=27/8, очевидно, не связывая еще квадратуру круга с кубатурой шара.

Известно, что отношение длины окружности к диаметру не может быть точно выражено ни целым числом, ни обыкновенной дробью, ни конечной десятичной дробью.

Приближенные с недостатком и избытком значения для Архимед получил, рассматривая вписанные в круг и описанные около него многоугольники с достаточно большим числом сторон. Он последовательно определял стороны вписанных и описанных шестиугольника, двенадцатиугольника, двацатичетырехугольника, сорокавосьмиугольника и девяностошестиугольника, выраженные через диаметр. Созданный Архимедом метод вычисления длины окружности посредством периметров вписанных и описанных многоугольников применялся многими видными математиками на протяжении почти 2000 лет.

В некоторых странах Азии встречается значение , т.е. 3,162…. астроном Ван Фань (229-267) утверждал, что , т.е. 3,155…, а Цзу-чжи (428-499) говорил о «неточном» значении и о «точном» , показав, что содержится между 3,1415926 и 3,1415927. Последнее значение записывалось в VII в. в виде именованного числа: 3 чжана 1 чи 4 цуня 1 фень 5 ли 9 хао 2 мяо 7 хо.

В индийских «сутрах» (VII-V вв. до н.э.) имеются правила, из которых вытекает, что =3,008. Ариабхатта и Бхаскара брали значение , т.е. 3,1416…, Брахмагупта, Магавира и Сриддхара брали .

В своей книге «Об измерении окружности» (1424) ал-Каши нашел для значение, далеко превосходящее по точности все ранее известные. Рассмотрев вписанный и описанный многоугольники с 800 335 168 сторонами, он получает окончательный результат, выраженный в шестидесятеричных и в десятичных дробях в виде 2 6,2831853071795865, т.е. 3,1415926535897932 – тут 16 верных знаков.

Однако труды ал-Каши в Европе долгое время не были известны. Голландский профессор Адриан Меций вновь нашел в XVI в. значение для независимо от Цзу Чун-чжи. В 1597 г. А. Ван Ромен из Лувена (Бельгия), применяя метод Архимеда с помощью 2³⁰-угольников, получил 17 верных десятичных знаков. Большое терпение и выдержку обнаружил голландский вычислитель Лудольф ван-Цейлен (1540-1610), который, применяя метод Архимеда, дошел до многоугольников с 60·20²⁹ степени сторонами, получив 35 верных десятичных знаков для . В его честь число было названо современниками «Лудольфово число». Согласно завещанию самого Лудольфа, на его надгробном камне было высечено найденное им значение .

Начиная с конца XVII в. для вычисления применяются более эффективные методы высшей математики. Леонард Эйлер вычислил с точностью до 153 десятичных знаков. После опубликования его работы (1736) стало общепринятым обозначение (первая буква в греческом слове «периферия» - круг), которое встречается впервые в 1706 г. у английского математика У. Джонса. В 1873 г. англичанин В. Шенкс определил с точностью до 707 десятичных знаков, усердно проработав для этой цели целых 15 лет. Однако, как выяснилось впоследствии, 527-й знак Шенкса оказался неверным. Ошибка была обнаружена Фергюссоном и Ренчем, которые в 1948 г. получили значение с 808 знаками. С помощью электронных машин в 1949 г. получено значение с 2035 знаками, а позднее – с 3089 знаками всего лишь за 13 с. К 1963 г. было найдено уже 100 265 десятичных знаков числа . Вычисление такого большого числа знаков для не имеет практического значения, а показывает лишь огромное преимущество и совершенство современных средств и методов вычисления по сравнению со старыми.