В полярных координатах

При вычислении определенного интеграла важную роль играет правило замены переменной, согласно которому при соблюдении соответствующих условий получаем

.

Обычно функция 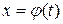монотонна. Она осуществляет взаимно однозначное соответствие между точками промежутка изменения переменной и точками промежутка изменения переменной 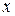. Делая замену по формуле 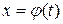, необходимо заменить на и вместо старых пределов и по переменной 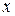взять им соответствующие новые пределы и по переменной .

Для упрощенного вычисления двойного интеграла также применяется метод подстановки. Но правило замены переменной в двойном интеграле значительно сложнее, чем в определенном интеграле. Приведем только окончательную формулу замены переменных в двойном интеграле и разъясним ее на примере преобразования к полярным координатам.

Определим преобразование независимых переменных 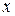и как

и .

Если функции и 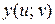имеют в некоторой области плоскости непрерывные частные производные первого порядка и отличный от нуля определитель

,

а функция непрерывна в области 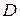, то справедлива формула замены переменной в двойном интеграле:

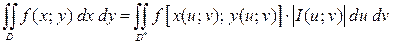. (1.4)

Сами новые переменные и называются криволинейными координатами. Различные системы криволинейных координат играют важную роль в математике и ее приложениях.

Функциональный определитель называется определителем Якоби или якобианом (Г. Якоби (1804 – 1851) – немецкий математик).

Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат 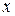и полярными координатами и .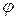

В качестве переменных и возьмем полярные координаты и 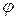. Они связаны с декартовыми координатами формулами , .

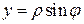Правые части в этих равенствах – непрерывно дифференцируемые функции. Якобиан преобразования определяется как

Формула замены переменных (1.4) принимает вид:

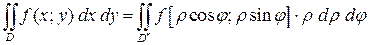, (1.5)

где - область в полярной системе координат, соответствующая области 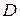в декартовой системе координат.

пересекает ее границу не более чем в двух точках. Тогда правую часть формулы (1.5) можно записать в виде повторного интеграла

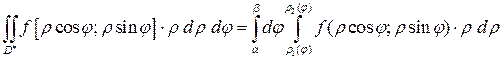. (1.6)

Внутренний интеграл берется при постоянном 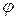. Формула (1.6) применяется, если полюс полярной системы координат находится вне области . В отдельных случаях формула (1.6) упрощается.

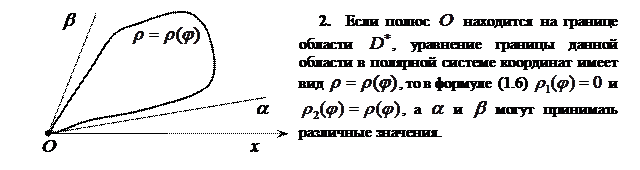
Пример 1.2. Вычислить 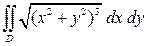, если область - круг .

Решение. Если область - круг или его часть, то интеграл проще вычислить в полярных координатах. Вводим замену: , 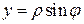. Тогда , . Область так же запишем в полярных координатах: или . Поскольку полюс находится внутри области , то , , и 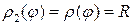. Согласно формуле (1.6) имеем

.

,