В декартовых координатах. Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов

Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.

Пусть требуется вычислить двойной интеграл , где функция 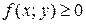непрерывна в области 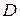. Тогда, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью 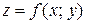. Найдем этот объем, используя метод параллельных сечений. Ранее было показано, что , где - площадь сечения плоскостью, перпендикулярной оси , а и - уравнения плоскостей, ограничивающих данное тело.

направлении оси : любая прямая, параллельная оси , пересекает границу области не более чем в дух точках.

Построим сечение цилиндрического тела плоскостью, перпендикулярной оси : , где .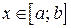

В сечении получаем криволинейную трапецию , ограниченную линиями 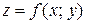, где , и . Площадь этой трапеции находим с помощью определенного интеграла:

.

Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:

.

С другой стороны, объем цилиндрического тела определяется как двойной интеграл от функции 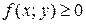по области 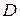. Следовательно,

.

Таким образом, для вычисления двойного интеграла функции 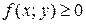по области 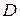используется следующая формула

. (1.2)

Правую часть (1.2) называют двукратным (или повторным) интегралом от функции по области . Интеграл называется внутренним интегралом.

Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая 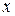постоянным, затем берем внешний интеграл, т.е. результат первого интегрирования интегрируем по 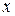в пределах от до .

Если область ограничена прямыми и (), кривыми и , причем для всех , т.е. область - правильная (стандартная) в направлении оси , то, рассекая тело плоскостью , аналогично получаем

. (1.3)

Здесь при вычислении внутреннего интеграла, считаем постоянным.

Замечания.

1. Формулы (1.2) и (1.3) справедливы и в случае, когда , .

2. Если область правильная в обоих направлениях, то двойной интеграл можно вычислять как и по формуле (1.2), так и по формуле (1.3).

3. Если область не является правильной ни «по 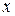», ни «по », то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси или оси .

4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.

Пример 1.1. Вычислить , если область ограничена линиями: .

Решение. I способ.

II способ. Построенная область является правильной в направлении оси . Для вычисления двойного интеграла воспользуемся формулой (1.3):

.

,