Билет 17

Обозначим через φ величину угла между прямыми и (напомним, что угол между прямыми измеряется от 0° до 90°), а через ψ – угол между нормальными векторами и этих прямых. Если ψ ≤ 90°, то φ = ψ. Если же ψ > 90°, то φ = 180° – ψ. В обоих случаях верно равенство 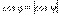Из теоремы 11.10 следует, что

и, следовательно,

Записав через координаты, получим

Если прямые и заданы уравнениями с угловыми коэффициентами и

и

то нормальные векторы этих прямых могут быть и выражение для косинуса угла между этими прямыми будет иметь вид:

Из последнего выражения следует, что если то cos φ = 1 и φ = 0, то есть прямые параллельны или совпадают. С другой стороны, если прямые параллельны, то φ = 0 или cos φ = 1. Подставляя в правую часть вместо cos φ его значение 1, умножая обе части на знаменатель и возводя в квадрат, получим

Отсюда получаем

Если то cos φ = 0 и то есть прямые перпендикулярны. Обратно, если прямые перпендикулярны, то или cos φ = 0. Отсюда следует с необходимостью

Следовательно, необходимые и достаточные условия параллельности и перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами и формулируются следующим образом.

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k ₁ = k ₂.

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

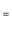
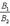
5. Условия перпендикулярности двух прямых:

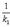
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е. Прямые с направляющими векторами а и b:

а) параллельны тогда и только тогда, когда векторы а и b коллинеарны;

б) перпендикулярны тогда и только тогда, когда векторы а и b перпендикулярны, т. е. когда а • b = 0.

Отсюда получаем необходимые и достаточные условия параллельности и перпендикулярности двух прямых, заданных каноническими уравнениями.

Для того чтобы прямые

были параллельны, необходимо и достаточно чтобы выполнялось условие В случае, если какое-либо из чисел b ₁, b ₂, b ₃ равно нулю, то должно обращаться в нуль соответствующее ему число a ₁, a ₂, a ₃. Для перпендикулярности прямых необходимо и достаточно, чтобы выполнялось условие

a ₁ b ₁ + a ₂ b ₂ + a ₃ b ₃ = 0.