Прямой метод Ляпунова

Данный метод позволяет судить об устойчивости непосредственно по уравнениям возмущенного движения, не прибегая к их интегрированию.
Уравнения возмущенного движения записываются в нормальной форме Коши в отклонениях от невозмущенного движения dx_i/dt = X_i(x₁,x₂…x_n) i=1…n.
Невозмущенному движению при этом соответствует тривиальное решение, т.е. x₁=x₂=..x_n=0.
Если X_i(x₁…x_n) представляют собой функции фазовых координат (отклонений), непрерывные в некоторой области Rⁿ, содержащей начало координат и имеющей частные производные по всем аргументам, то для анализа устойчивости невозмущенного движения могут быть использованы специальные функции фазовых координат, называемые функциями Ляпунова.
Прямой метод опирается на известную теорему Лагранжа, согласно которой равновесие устойчиво, если в положении равновесия потенциальная энергия системы минимальна.
Идея метода состоит в том, чтобы подобрать такую функцию фазовых координат, которая бы в некотором смысле была аналогична потенциальной энергии системы в состоянии покоя.

Рядом специальных свойств обладают функции Ляпунова. Это непрерывные однозначные функции фазовых координат, определенные в области Rⁿ Σx_j²≤ μ (15) (μ- постоянное положит. число), удовлетворяющие условию V(x₁…x_n)=0 при x₁=x₂=…x_n=0 (16) и имеющие производные по всем аргументам. Цель состоит в том, чтобы, предполагая невозмущенное движение устойчивым, попытаться подобрать такую функцию фазовых координат, которая при любом движении системы уменьшалась, т.е dV/dt<0.
Если в окрестности начала координат функция V кроме нуля может принимать значения только одного знака, то она называется знакопостоянной (положительной или отрицательной)
Если знакопостоянная ф-я обращается в нуль только в том случае, когда все x₁…x_n равны нулю, то ф-я V называется знакоопределеной (определенно-положительная или определенно-отрицательная)
Знакоопределенная функция имеет при x₁=…x_n=0 экстремум (min для опред.-положит. функции и mах для опред.-отриц). Знакопостоянная ф-я в начале координат экстремума не имеет, т.к. в окрестности начала координат есть точки, в котoрых V=0.

Пусть V=V(x) непрерывна вместе с производными первого порядка: кроме того предположим, что V(x) знакоопределенная.
Тогда при x₁=…x_n=0 она будет иметь изолиров. экстремум и все

Разложим V в ряд Маклорена по степеням x₁…x_n

Учитывая (16) и (17), получим Обозначим

Т.о. разложение знакоопределенной функции V в ряд по степеням x₁…x_n не содержит членов первой степени, т.е. остается квадратичная форма:

Пусть квадратичная форма принимает положительные значения и в нуль обращается только при x₁=…x_n=0. Тогда вне зависимости от членов высшего порядка при достаточно малых по модулю x_j функция V будет принимать тоже положительные значения и в нуль обращается только при x₁=…x_n=0.
Если квадратичная форма (21) определенно – положительна, то и функция будет определенно положительной.
Рассмотрим матрицу коэффициентов квадратичной формы (21) и составим из нее n главных диагональных миноров.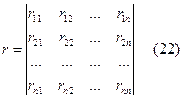

В линейной алгебре доказывается следующий критерий Сильвестра:
Для того, чтобы квадратичная форма была определенно-положительной, необходимо и достаточно, чтобы все главные диагональные миноры матрицы ее коэффициентов были положительны, т.е. Δ₁>0, Δ₂>0… Δ_n>0 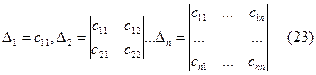. Для того, чтобы квадратичная форма была определенно-отрицательной, необходимо и достаточно, чтобы имели место неравенства Δ₁<0, Δ₂>0, Δ₃<0, т.е. oпределители должны последовательно чередовать знак, причем знак Δ₁=c₁₁ д.б. отрицательным.

Критерий Сильвестра для квадратичной части функции V является достаточным (но не необходимым) условием определенной положительности самой функции V.

41. Компьютерные модели в автоматизированном управлении

Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить т.н. вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов), в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и начальных условий.

Построение компьютерной модели базируется на абстрагировании от конкретной природы явлений или изучаемого объекта-оригинала и состоит из двух этапов - сначала создание качественной, а затем и количественной модели. Компьютерное же моделирование заключается в проведении серии вычислительных экспериментов на компьютере, целью которых является анализ, интерпретация и сопоставление результатов моделирования с реальным поведением изучаемого объекта и, при необходимости, последующее уточнение модели и т. д.

К основным этапам компьютерного моделирования относятся:

постановка задачи, определение объекта моделирования;

разработка концептуальной модели, выявление основных элементов системы и элементарных актов взаимодействия;

формализация, то есть переход к математической модели; создание алгоритма и написание программы;

планирование и проведение компьютерных экспериментов;

анализ и интерпретация результатов.

Различают аналитическое и имитационное моделирование. При аналитическом моделировании изучаются математические (абстрактные) модели реального объекта в виде алгебраических, дифференциальных и других уравнений, а также предусматривающих осуществление однозначной вычислительной процедуры, приводящей к их точному решению. При имитационном моделировании исследуются математические модели в виде алгоритма(ов), воспроизводящего функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций.

42. Моделирование и подобие; динамические аналогии; критерии подобия. Пи-теорема.

Теория подобия и моделирования.

Подобие Подобие Подобие

геометрическое скоростей и ускор. динамическое

p - критерий подобия; безразмерная величина, но является отношением размерных величин.

M = v/a

- число Маха, отношение скорости объекта к скорости звука.

Если М<1, то - докритическое течение,

при М>1 происходят скачки уплотнения.

М=1- граница между надкритическим и докритическим течениями,

которые качественно отличаются.

Критерий Рейнольдса

Re = dwr/m

d - диаметр;

w - скорость потока;

r - плотность;

m - динамическая вязкость.

Движение жидкости в трубе

w d Ламинарное течение (слоистое).

Линейная зависимость между P и Q.

w d Турбулентное течение.

Нелинейная зависимость между P и Q.

Если Re < 2300, то ламинарное течение;

Re > 2300, то турбулентное течение.

При ламинарном и турбулентном течениях работают разные формулы.

Отдельные Идея

признаки (гипотеза)

аналогии сходства

Отдельные Известный

признаки результат

(хорошо отработаны)

Т.е. при изучении новой системы мы проводим аналогии и по подобию к уже известной системе строим интересующую нас систему.

Методы получения критериев подобия.

Метод основан на использовании:

а). p - теоремы (теоремы Букингема)

б). Метода интегральных аналогов

В основе лежит теория размерности.

A = {A}[A]

[A] - единицы размерности, т.е.

A = {30}[км/час]

Есть единицы основные и произвольные.

Пример

Определение коэффициента лобового сопротивления.

Дано: Труба с водой (модель);

Характерный размер d;

Значения параметров r; w; m.

d

Наименование	Обозначение	Размерность
Скорость	w	Lt-1
Характерный признак	d	L
Плотность среды	r	ML-3
Вязкость динамическая	m	Mt-1L-1
Сила лобового сопротивления	F	MLt-2

Есть некая функция, которая определяет силу лобового сопротивления как

j(w^a, d^b, r^c, m^l) = F

Определим размерность

j([Lt^-1]^a, [L]^b, [ML^-3]^c, [Mt^-1L^-1]^l) = [MLt^-2]

M: c + l = 1

L: a + b - 3c - l = 1

t: - a - l = -2

Решаем систему уравнений и получаем

c = 1 - l

a = 2 - l

2 - l + b - 3 + 3l - l = 1

b = 2 - l

Перепишем исходную формулу в несколько ином виде

j(w^2-l, d^2-l, r^1-l, m^l) = F

т.е. можем записать

F/w²d²r = j¢(m/wdr) = j¢(1/Re)

p - теорема

Всякое полное уравнение физического процесса записанное в определенной системе единиц может быть представлена в виде зависимости между критериями подобия, т.е. безразмерных соотношений, составленных из входящих в уравнение переменных и параметров.

f(P₁, P₂,..., P_i,..., P_k,..., P_s,..., P_m) = 0

1 £ i £ k k+1 £ s £ m f(P₁/P₀₁;P₂/P₀₂,...;P_i/P_0i,...;P_k/P_0k,...;P_s/P_0s,...;P_m/P_0m)=0

Основные и производные единицы. Производные можно выразить через основные.

Для этого надо:

а) Выбрать те параметры, которые являются независимыми.

Б) Выразить зависимые через независимые. Имеем матрицу размерностью [m´n], в которой число строк больше числа столбцов (m > n).

Ранг не больше n.

Пусть

P₁,..., P_k - независимые параметры;

P_k+1,..., P_m - зависимые параметры.

P_k+1,..., P_m. следует выразить через P₁,..., P_k

Тогда получим

f(1,...,1, p ₁,..., p_s-k,..., p_m-k) = 0

Каждый параметр P выражается в виде

Р = {Р}[Р]

где {Р}- число, [Р] - размерность.

[P₁] = [a^a1, b^b1,..., q^x1] = [P₀₁]

[P₂] = [a^a2, b^b2,..., q^x2] = [P₀₂]

...........

[P_i] = [a^ai, b^bi,..., q^xi] = [P_0i]

...........

[P_k] = [a^ak, b^bk,..., q^xk] = [P_0k]

k £ q

q - количество независимых параметров.

[P_0,k+1] = y_k+1{[P₀₁],...,[P_0k]}

..........

[P_0,s] = y_s{[P₀₁],...,[P_0k]}

..........

[P_0,n] = y_n{[P₀₁],...,[P_0k]}

Определим зависимости y_k+1,...,y_s,...,y_n

ln[P₀₁] = a₁ln[a] + b₁ln[b] +...+ x₁ln[q]

ln[P₀₂] = a₂ln[a] + b₂ln[b] +...+ x₂ln[q]

...............

ln[P_0k] = a_kln[a] + b_kln[b] +...+ x_kln[q]

a₁ b₁ ... x₁ ln[P₀₁]

a₂ b₂ ... x₂ = D ln[P₀₂]

........

a_k b_k... x_k ln[P_0k]

D - определитель

ln[a] = (ln[P₀₁])^A11/D(ln[P₀₂])^A21/D´...´(ln[P_0k])^Ak1/D

A_k1 - определить получаемый из определителя D путем вычеркивания k-ой строки и 1-го столбца.

_k

ln[a] = å(A_i1/D)ln[P_0i]

ⁱ⁼¹

Пусть k = q

ln[a] =

ln[b] =

....

ln[q] =

Определяем [a],[b],...,[q]

[a] = [P₀₁]^A11/D[P₀₂]^A21/D´...´[P_0k]^Ak1/D

[b] =

...

[q] =

Полученные выражения подставим в формулы

[P_0,k+1] = [P₀₁]^D1,k+1/D[P₀₂]^D2,k+1/D... [P_0k]^Dk,k+1/D

..........

[P_0,s] = [P₀₁]^D1,s/D[P₀₂]^D2,s/D... [P_0k]^Dk,s/D

..........

[P_0,m] = [P₀₁]^D1,m/D[P₀₂]^D2,m/D... [P_0k]^{Dk, m/D}

D_i,k+1 - определитель, в котором i-ая строка заменена (k+1) строкой из формул размерности. _k

[P_0,s] = Õ[P_0i]^Di,s/D

ⁱ⁼¹

Di,k+1/D = x_i

Di,s/D = y_i

Di,m/D = z_i

_k

[P_0,k+1] = Õ[P_0i]^xi = p ₁

ⁱ⁼¹

_k

[P_0,s] = Õ[P_0i]^yi = p_s-k

ⁱ⁼¹

_k

[P_0,m] = Õ[P_0i]^zi = p_m-k

ⁱ⁼¹

Пусть

P₁ = P₀₁

P₂ = P₀₂

....

P_k = P_0k

_{k k k}

f(1,...,1, P_k+1/Õ[P_0i]^xi,...,P_s/Õ[P_0i]^yi,..., P_m/Õ[P_0i]^zi) = 0

^{i=1 i=1 i=1}

f(1,...,1, p₁,..., p_s-k,..., p_m-k)

p₁ = j(p₂,..., p_m-k)

Реальность Модель

p₁ p₁

p₂ p₂

......

p_m-k p_m-k

P₁, P₂,...,P_k,...,P_m

- подобие сил.