Метод главных компонент

Весьма часто исследователю приходится ограничиваться пассивным экспериментом.

Постановка задачи.

Пусть эксперимент заключается в наблюдении некоторого к-мерного вектора-строки независимых переменных

х^* = (х₁, х₂,........ х_к)

Если экспериментатор имеет возможность

N наблюдений над различными значениями вектора-строки х^*, то результаты его исследования представляются матрицей:

Во многих случаях кажется естественным предположить, что в изучаемой плохо организованной системе существует некоторое количество непосредственно не наблюдаемых, но легко интерпретируемых переменных, ответственных за поведение вектора Х^*.

Тогда исследователю может понадобиться выразить полученную им при наблюдении информацию через эти, непосредственно не наблюдаемые переменные, т.е. не соответствуют два типа информации, требуемой для модели и фиксируемая.

Для осуществления такого перехода к новым переменным нужно использовать внутреннюю структуру матрицы Х.

Статистические свойства этой матрицы, (если выполнять нормальное распределение), задаются ковариационной матрицей

МЕТОД ГЛАВНЫХ КОМПОНЕНТ

Предложен в 1901г. Пирсоном. Детально разработан Хоттелингом в 1933г.

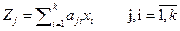Новые переменные – главные компоненты. В методе главных компонент ищут некоррелированные нормированные линейные комбинации,

дисперсии которых расположены в убывающем порядке, т.е. S²(Z₁)≥ S²(Z₂) ≥ S²(Z₃) ≥...., ко- вариационная матрица оказывается расщепленной на к- ортогональных компонентов.

На языке матричной алгебры – коэффициент линейных комбинаций – компоненты собственных векторов корреляционной матрицы, дисперсии главных компонент – собственные числа,т.е.

S²(Z_i) = λ_i, которые удовлетворяют уравнению:

/R - λ I / = 0, некоторому значению λ_i соответствует собственный вектор а_i, т.е. векторы-столбцы а_i, удовлетворяющие равенству Ra_i = λ_ia_i

Справедливы следующие соотношения:

а_i ^тa_i = 1 (условие нормировки)

а_i ^тa_J = 0(условие ортогональности)

Переход к новым координатам в матричной форме записывается Z = A^тx (А- матрица со столбцом собственных векторов а).

Ковариационная матрица ZZ^т – диагональная (ортогональность главных компонент) с диагональными элементами λ_i.

Геометрически нахождение главных компонент сводится к переходу к новой ортогональной системе координат: первая координатная ось ищется так, чтобы соответствующая ей линейная форма извлекла возможно большую дисперсию.

Далее ищется ортогональная ей ось и

от новых координат можно вернуться к старым, записав (учитывая ортогональность преобразования):

где Z_j – означает j-ую главную компоненту, а а_ji – вес j-той компоненты в i-той переменной.

Это основное выражение в методе главных компонент. Оно не содержит остаточной составляющей ε_i, т.к. вес «к» - главных компонент исчерпывают всю дисперсию исходных переменных.