Корреляционный анализ изучает на основании выборки стохастическую зависимость между случайными переменными

Коэффициент множественной корреляции. (сводный коэф. корреляции)
Используется для описания системы сл. в-н {Х₁,Х₂…Х_n}. Служит характеристикой корреляции между величиной Х₁ с одной стороны и всей совокупностью величин (Х₂,Х₃…Х_n) с другой.

Р – детерминант квадратной матрицы коэф. коррел.
Р₁₁ – минор этого детерминанта

При n=3

Свойства
1. всегда является положительным числом 0≤r_1(23..n) ≤1
2. при r_1(23..n)=1 случайная величина Х₁ почти наверное равна линейной комбинации Х₂,Х₃…Х_n.
3. равенство r_1(23..n)=0 имеет место тогда, когда r₁₂,r₁₃,…r_1n=0, т.е. случайная величина Х₁ не коррелированна со всеми остальными случайными величинами системы.

Частные (парциальные) коэф. корреляции
характеризуют тесноту связи между двумя случайными величинами системы при исключении влияния остальных случайных величин.
Частный коэф. корреляции в-н Х₁ и Х₂, входящих в систему {Х₁,Х₂…Х_n} относительно в-н Х₃, Х₄, …Х_n обозначается через r_12,34…n

где Р₁₂- минор детерминанта квадратной матрицы
(матрицы коэф. корреляции), получаемой путем вычеркивания 1^ой строки и 2^го

столбца, умноженной на (-1)¹⁺²=-1

В отличие от коэф. множеств. корреляции коэф. частной корреляции, как коэф. парной корреляции меняется в пределах от -1 до +1.
Пи наличии корреляции частный коэф. корреляции r_12,34…n в общем случае не равен коэф. парной корреляции r₁₂.

1. Метод ранговой корреляции по Спирмэну

Мера зависимости между случайными величинами (наблюдаемыми признаками, переменными), когда эту зависимость невозможно определить количественно с помощью обычного коэффициента корреляции. Процедура установления ранговой корреляции заключается в упорядочении изучаемых объектов в отношении некоторого признака, т. е. им приписываются порядковые номера — ранги (по два номера в соответствии с двумя наблюдаемыми признаками, между которыми исследуется корреляция). Например, наибольшее значение для переменной обозначается номером 1, второе по величине — номером 2 и т. д. Наиболее распространен коэффициент ранговой корреляции (коэффициент Спирмэна):

где D _i — разница между рангами, присвоенными каждой из переменных i (i = 1, 2,..., n); N — размер выборки. Этот коэффициент принимает значения в интервале от +1 до –1, показывая силу и направление связи между исследуемыми величинами.

15- 16. Матричная форма МНК при построении моделей …

МНК имеет три этапа:
1 этап Определение коэффициентов а.
2 этап Оценка достоверности коэффициентов а.
3 этап Проверка адекватности модели.
= (a0...ak)¢ - вектор- столбец
x = (x1...xk)¢ - вектор- столбец
f(x) = (1, x1,.., xk)¢
- наблюдаемые значения, – оценки, - истинные значения

Эксперимент проводится в N точках, т.о. фиксируем x и y. x1, x2,..., xN - точки экспериментов.
xi= (xi1, xi2,..., xin)¢ 1 £ i £ N
- вектор наблюдений функции отклика.

Для оценки адекватности модели в любой точке xi эксперимент повторяется n раз.

Информационная матрица

- ошибка, погрешность.

Требуемые условия.
1. Результаты наблюдений свободны от систематических ошибок

E - математическое ожидание.
2. Результат наблюдений в точке xj не зависит от результата наблюдений в точке xi.

3. Дисперсия результатов наблюдений во всех точках одинакова.
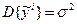для любых i.
4. Оценка является несмещенной

5. Дисперсия оценки должна быть минимальна

где - оценка, которая еще пока не найдена.

Так как ¶S/¶a = 0 то следовательно

14. Корреляционное отношение.

Применение коэф. корреляции ограничивается случаем линейной связи. Для оценки нелинейной связи используют корреляционное отношение. Корреляционное отношение требует расчета условных дисперсий.
Зависимость Dу׀х = φ(х) – скедастическая функция. Если φ(х)=const, то условная дисперсия переменной У –постоянна, не зависит от х и говорят, что связь между случайными переменными у и х гомоскедастическая.
Чтобы получить представление о рассеянии случайной переменной у во всем диапазоне изменения переменной Х1используют вероятностную, называемую средней условной дисперсией . По гомоскедастической связи, когда Dу׀х =const, то ничем не отличается от Dу׀х. По определению

Установим соотношение между полной дисперсией Dyи средней условной дисперсией . Формула полной дисперсии случайной переменной у записывается в виде
Dy= M[ y2]-m2y, my= M[y]
Cделаем искусственное преобразование. Прибавим и отнимем от правой части M[m2ylx], где mylx= M[y l x] -условное мат.ожидание
Dy= M[ y2 ] - M[m2ylx] + M[m2ylx] - m2y
Вспомним, что = M[ y2] - M[ m2ylx]
M[m2ylx] - m2y= D{M[ylx]}
Это следует из D{M[ylx]} = D[mylx] = M[m2ylx] - {M[mylx]}2 = M[m2ylx]-m2y,
т.е. Dy= + D{M[ylx]} Это формула разбиения дисперсий.

Т.е. полная дисперсия является суммой средней условной дисперсии и дисперсии условного математического ожидания. Поясним это.
Если х – входная, а у – выходная переменные, то дисперсия условного мат. ожидания D{M[ylx]} представляет собой ту часть полной дисперсии Dyвыходной переменной у, которая связана с влиянием входной переменной х.
Вторая часть полной дисперсии – средняя условная дисперсия – определяется влиянием совокупности всех остальных переменных, кроме учтенной переменной х.
Так как = Dy– D{M[ylx]}, то ≤Dy. Равенство имеет место, когда D{M[ylx]} = 0
В качестве меры корреляц. отношения принято η2yx=1 - / Dy; ηyx– корреляц. отношение

Свойства: 1. 0 ≤ ηyx≤ 1; 0 ≤ ηxy≤1. Это свойство следует из формул
ηyx=1- /Dy ηxy= 1- /Dx аналогично
η2yx= D{ M[ylx] } / Dy η2xy= D{ М[xly] } / Dx
2. Величина η всегда положительна.
3. Равенство ηyx= 0 означает, что переменная y не коррелированна с переменной x. Если x и y – независимы, то ηyx= 0.
4. Равенство ηyx=1 соответствует функциональной связи между y и x.
5. В общем случае ηyx≠ ηxy, т.е. данная связь несимметрична

6. Если связь между переменными x и y линейна, то ηyx= ηxy.
7. При линейной регресии ηyx= ׀ryx׀, т.е. корреляционное отношение служит характеристикой и линейной связи.
8. При линейной регрессии всегда ηyx> ׀ryx׀, т.е. коэффициент корреляции при нелинейной стохастической связи дает заниженные оценки.
Разность η2yx-r2yx=h2yx– индикатор степени нелинейности стохастической связи.

17. Матричная форма МНК при построении модели (этап проверки адекватности полученной модели)

Проверка адекватности модели.
Н₀: t_р £ t_кр
где t_р - расчетное значение
t_кр - табличное значение

1- a = р
a
В основе проверки адекватности модели лежит сопоставление достигнутой точности модели с точностью наблюдения. Для оценки точности используем дисперсию, поэтому необходимо сравнить дисперсию ошибки по модели с дисперсией ошибки наблюдений. Поэтому в каждой точке эксперимент повторяется n раз.

отсюда следует, что

Дисперсия ошибки моделирования.

Дисперсия ошибки наблюдения

Далее рассчитываем статистику Фишера F_р = (S_D/j₁)/(S_e/j₂)
Если ошибка моделирования меньше ошибки наблюдения, то модель хорошая.
Выдвигается гипотеза Н₀. Определяется уровень значимости a.
В соответствии с a, j₁ и j₂ из таблицы находим F_кр.
P{ïFï < F_кр} = 1-a
f_F

F
F_p F_кр

Если F_p £ F_кр, то модель адекватна.

1. Проблема оценки адекватности моделей

Реально отличается от.
Дисперсия - мера отличия. Чем больше дисперсия, тем больше отличие.
Дисперсия будет зависеть как от дисперсии ошибок наблюдения σ², так и от точек постановки опытов.

- ковариационная матрица.

Поставим вместо а ее оценку и с учетом условий запишем все необходимые выражения.

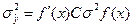Так как корреляционная матрица симметрична, то при - дисперсия коэффициента а_i

Действует нормальный закон распределения.

- стандартное отклонение

19. Общий подход к составлению статистических оценок.

Статистические оценки - функции от результатов наблюдений, употребляемые для статистического оценивания неизвестных параметров распределения вероятностей изучаемых случайных величин.

Например, если X₁,..., X_n — независимые случайные величины, имеющие одно и то же Нормальное распределение с неизвестным средним значением а, то функции — среднее арифметическое результатов наблюдений

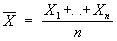
и выборочная Медиана μ = μ(X₁,..., X_n) являются возможными точечными С. о. неизвестного параметра а. В качестве С. о. какого-либо параметра θ естественно выбрать функцию θ^*(X₁,..., X_n) от результатов наблюдений X₁,..., X_n, в некотором смысле близкую к истинному значению параметра. Принимая какую-либо меру «близости» С. о. к значению оцениваемого параметра, можно сравнивать различные оценки по качеству. Обычно мерой близости оценки к истинному значению параметра служит величина среднего значения квадрата ошибки

(выражающаяся через Математическое ожидание оценки E₀θ* и её дисперсию D₀θ*). В классе всех несмещённых оценок (для которых E₀θ* = 0) наилучшими с этой точки зрения будут оценки, имеющие при заданном n минимальную возможную дисперсию при всех θ. Указанная выше оценка Х для параметра а нормального распределения является наилучшей несмещенной оценкой, поскольку дисперсия любой другой несмещенной оценки а* параметра а удовлетворяет неравенству ² — дисперсия нормального распределения. Если существует несмещенная оценка с минимальной дисперсией, то можно найти и несмещенную наилучшую оценку в классе функций, зависящих только от достаточной статистики. Имея в виду построение С. о. для больших значений n, естественно предполагать, что вероятность отклонений θ* от истинного значения параметра θ, превосходящих какое-либо заданное число, будет близка к нулю при n →∞. С. о. с таким свойством называются состоятельными оценками. Несмещенные оценки, дисперсия которых стремится к нулю при n →∞, являются состоятельными. Поскольку скорость стремления к пределу играет при этом важную роль, то асимптотическое сравнение С. о. производят по отношению их асимптотической дисперсии. Так, среднее арифметическое Х в приведённом выше примере — наилучшая и, следовательно, асимптотически наилучщая оценка для параметра а, тогда как выборочная медиана μ, представляющая собой также несмещенную оценку, не является асимптотически наилучшей, т.к.

(тем не менее использование μ имеет также положительные стороны: например, если истинное распределение не является в точности нормальным, а несколько отличается от него, дисперсия Х может резко возрасти, а дисперсия μ остаётся почти той же, т. е. μ обладает свойством, называется «прочностью»). Одним из распространённых общих методов получения С. о. является метод моментов, который заключается в приравнивании определённого числа выборочных моментов к соответствующим моментам теоретического распределения, которые суть функции от неизвестных параметров, и решении полученных уравнений относительно этих параметров. Хотя метод моментов удобен в практическом отношении, однако С. о., найденные при его использовании, вообще говоря, не являются асимптотически наилучшими, Более важным с теоретической точки зрения представляется Максимального правдоподобия метод, который приводит к оценкам, при некоторых общих условиях асимптотически наилучшим. Частным случаем последнего является Наименьших квадратов метод. Метод С. о. существенно дополняется оцениванием с помощью доверительных границ.

20. Составление статистических оценок; анализ наиболее часто используемых законов распределения. Закон распределения Стьюдента.

Статистики

Параметрические Непараметрические
(нормальный) неизвестен закон распределения малый объем выборки

Должны работать критерии согласия (сравнивают кривые распределения c2, Колмогорова - Смирнова).

Сравнение двух выборок
а). по среднему арифметическому (распределение Стьюдента)
б). по дисперсии (распределение Фишера, при малом объеме выборки - критерий Манна - Уитни)

Основные законы распределения,
используемые при составлении статистики.

- Теория вероятностей
- Математическая статистика
N ® ¥

Практические задачи.
Сравнить работу двух установок, если имеется некоторая статистика по обеим установкам.
1. Н₀ Н_альтер.
2. Сформировать статистику
3. Законы распределения

Распределение Стьюдента (Госсета).

Стьюдент доказал, распределение отношения разностей между выборочным средним и средним значением генеральной совокупности к стандартной ошибке среднего значения генеральной совокупности тогда и только тогда подчиняется нормальному закону распределения, когда s является стандартным отклонением единичного значения от среднего значения генеральной совокупности.

Если параметры m и s неизвестны, то в качестве оценки s нужно использовать s и тогда мера отклонения t будет определяться таким образом:

t - распределение и N – нормальный закон распределения в чем-то похожи

t - непрерывно, симметрично,
колоколообразно, с областью
определения функции [-¥; +¥]

Число степеней свободы.
n = n - k
n - число степеней свободы
n - объем выборки
k - число формул