 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры. Если равные дроби имеют одинаковые знаменатели, то и числители их одинаковы, т.е
|
|
1. 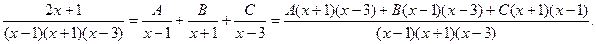
Если равные дроби имеют одинаковые знаменатели, то и числители их одинаковы, т.е.
2х+1=А(х+1)(х-3)+В(х-1)(х-3)+С(х-1)(х+1) (**)
Положим х=1, тогда 
х=-1, тогда 
х=3, тогда 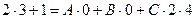
Имеем 3= -4А 
-1= 8В 
7= 8С 

Второй способ нахождения А,В,С состоит в сравнении коэффициентов при одинаковых степенях «х» в левой и правой частях равенства (**).
2. 
Под знаком интеграла стоит неправильная дробь, т.к. степень многочлена в числителе больше степени многочлена в знаменателе. Выделяем целую часть, разделив числитель на знаменатель. Подставляем это выражение в интеграл:
 , (2)
, (2)
Теперь под знаком интеграла стоит правильная дробь  , знаменатель которой разлагается на множители:
, знаменатель которой разлагается на множители:
(х3+1)=(х+1)(х2-х+1), причем х2-х+1 не имеет действительных корней, поэтому
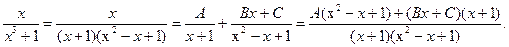
х= А  +(Вх+С)(х+1)
+(Вх+С)(х+1)
х=-1 -1=А(1-(-1)+1)  А=
А= 
х=0 0=А+С  С=
С= 
х=1 1=А+(В+С)  В=
В= 
Итак,  поэтому
поэтому 

 (3),
(3),
где J=  .
.
Выделяем полный квадрат в знаменателе: 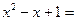

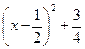 и делаем подстановку
и делаем подстановку  Приходим к результату:
Приходим к результату:
 (формула 13 ТОИ) =
(формула 13 ТОИ) =  Подставляя это в равенство (3), получаем:
Подставляя это в равенство (3), получаем:
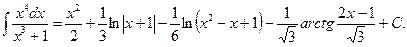
Дата публикования: 2015-07-22; Прочитано: 366 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
