Определение

Матрица А, i-тый столбец которой есть координатный столбец вектора относительно базиса (1), называется матрицей линейного оператора 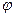в базисе (1).

Так как вектор пространства однозначно выражается через координатный базис, то матрица А линейного оператора 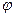относительно этого базиса определяется однозначно.

Обратно, пусть задана произвольная квадратная матрица А n- ного порядка над Р. Принимая i -тый столбец матрицы за координаты вектора в базисе (1), получим:

Существует единственный линейный оператор 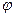пространства V(P), такой, что Таким образом, с заданием координатного базиса в пространстве V(P) устанавливается взаимно однозначное соответствие между множеством линейных операторов пространства V(P) и множеством квадратных матриц n- ного порядка над P.

Задача. Доказать, что существует единственный линейный оператор, переводящий векторы в 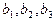соответственно. Найти его матрицу в единичном базисе.

Решение. Проверим, что линейно независимы. Для этого составим матрицу из векторов-строк приведем ее к ступенчатому виду, определим ранг.

то есть линейно независимы, они составляют базис трехмерного арифметического пространства, поэтому существует единственный линейный оператор 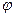пространства такой, что

Выразим через

Найдем .

= 2 b ₁- 5 b ₂- 4 b ₃ = 2(1, 1, 1) - 5(1, 1, -1) - 4(2, 1, 2) = (-11, -7, -1) =

= -11 e ₁ - 7 e ₂- e ₃.

Составляем матрицу оператора 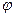в единичном базисе, располагая координаты в единичном базисе в i -ый столбец матрицы; i =1, 2, 3.

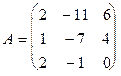
§ 4. Связь между координатными столбцами векторов х и

Пусть — базис . Возьмем любой

Как найти координаты если известны координаты вектора х и матрица А оператора 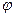в базисе ?

Так как координаты вектора в данном базисе определяются однозначно, то

Запишем полученную систему в матричной форме:

, то есть .