 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема. Пусть U(P) и V(P) — векторные пространства над одним и тем же полем Р;
|
|
Пусть U(P) и V(P) — векторные пространства над одним и тем же полем Р;
 — базис U(P),
— базис U(P),  — произвольные векторы из V(P).
— произвольные векторы из V(P).
Тогда существует единственное линейное отображение  удовлетворяющее условиям
удовлетворяющее условиям  (1)
(1)
Доказательство  .
.
Отображение  определим равенством
определим равенством
 для любых
для любых 
Отображение 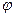 удовлетворяет условиям (1).
удовлетворяет условиям (1).
Например, при  получаем
получаем 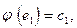 и т.д.
и т.д.
Докажем линейность отображения 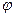 .
.




По определению отображения 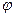


=  таким образом,
таким образом, 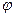 — линейное отображение.
— линейное отображение.
Предположим, что  : U® V — это линейное отображение, удовлетворяющее условиям
: U® V — это линейное отображение, удовлетворяющее условиям 
Для любого вектора 

 то есть
то есть 
Следствие 1. Пусть U(P), V(P) — векторные пространства,  — базис U;
— базис U; 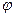 и
и  — линейные отображения U в V, такие, что
— линейные отображения U в V, такие, что  Тогда
Тогда  .
.
Следствие 2. Пусть  — базис V(P),
— базис V(P),  — произвольные векторы из V. Существует единственный линейный оператор
— произвольные векторы из V. Существует единственный линейный оператор  удовлетворяющий условиям (1).
удовлетворяющий условиям (1).
Дата публикования: 2015-07-22; Прочитано: 249 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
