 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Оператором
|
|
2. 
зафиксируем. Рассмотрим отображение 
такое, что 
есть линейный оператор пространства V. В самом деле, для любых 
и любого 
Оператор называется оператором гомотетии с коэффициентом 
. При 
получим нулевой оператор, при 
получим тождественный оператор.
3. Выясним, будет ли линейным отображение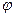 
пространства 
в себя, если для любого вектора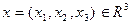 
.
Проверим выполнимость условий из определения линейного отображения для 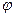. Возьмем любые 
любое 
то есть первое требование выполняется.
то есть второе требование выполняется.
Таким образом, 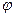— линейный оператор пространства 
Дата публикования: 2015-07-22; Прочитано: 240 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
