 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теоретические частоты
|
|
| Методика | Слабое | Удовлетворительное | Хорошее | всего |
| Первая (теоретические) | 60×(21/60)× (31/60)= 10,85 | 60×(19/60)×(31/60)= 9,82 | 60×(20/60)×(31/60)= 10,33 | |
| Первая (наблюдение) | ||||
| Вторая (теоретические) | 60×(21/60)× (29/60)= 10,15 | 60×(19/60)×(29/60)= 9,18 | 60×(20/60)×(29/60)= 9,67 | |
| Вторая (наблюдение) | ||||
| Всего |
Разумеется, полученные теоретические частоты отличаются от наблюдаемых. Но насколько значимо это отличие? Ответ дается критерием согласия Пирсона.
Критерий согласия К. Пирсона (критерий хи-квадрат) служит для проверки гипотезы о предполагаемом законе неизвестного распределения. Нулевая гипотеза: генеральная совокупность распределена по закону В (в нашем примере: pij = pi pj). Для проверки гипотезы сравниваются эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нулевой гипотезы) частоты. Если генеральная совокупность распределена по закону В, то указанная далее статистика имеет распределение хи-квадрат с определенным числом степеней свободы.
Для проверки при данном уровне значимости a нулевой гипотезы Н0, состоящей в том, что исследуемые признаки независимы, – следует выполнить следующие действия.
1. Вычислить теоретические (ожидаемые) частоты 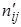 .
.
2. «Вычислить наблюдаемое значение критерия»:
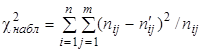 .
.
Таблица 3.
Дата публикования: 2014-10-25; Прочитано: 398 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
