Непрерывность

Действительная функция f: X ® Y непрерывна в точке x₀ Î X, если для любого числа e > 0 существует такое число d = d(e) > 0, что для всех точек х, удовлетворяющих условию |х – х₀| < d, выполняется неравенство

|f(x) – f(x₀)| < e.

Формальная запись: "e $d |х – х₀| < d Þ |f(x) – f(x₀)| < e

Иными словами, непрерывная в точке х₀ функция f имеет в качестве своего предела свое значение в точке х ₀, т. е.

Это равносильно тому, что

,

где Dх = х - х ₀ – приращение аргумента, а Dy = f (x) – f (x ₀) – приращение функции, соответствующее Dх.

В терминах предела последовательности эквивалентное определение непрерывности в точке х ₀ звучит так: для любой последовательности { x _n}, , имеет место равенство:

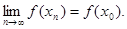
Функция f называется непрерывной справа в точке х₀, если

.

Аналогично определяется понятие непрерывной слева функции в точке х₀.. Функция f называется непрерывной на отрезке [a,b], если одновременно:

1) она непрерывна в каждой внутренней точке х, а < x < b;

2) она непрерывна справа в точке а;

3) она непрерывна слева в точке b.

Следующие теоремы выражают свойства непрерывных функций:

1) Действительная функция, непрерывная на отрезке, ограничена на нем (первая теорема Вейерштрасса).

2) Действительная функция, непрерывная на отрезке, принимает на нем свои наибольшее и наименьшее значения (вторая теорема Вейерштрасса).

3) Действительная функция, непрерывная на отрезке, принимает на нем любое значение, заключенное между значениями, которые она принимает на концах отрезка (теорема Коши).

4) Действительная функция, непрерывная на отрезке и строго монотонная на нем, обладает единственной обратной функцией, которая также определена на отрезке (области значений исходной функции), непрерывна и строго монотонна на нем (теорема об обратной функции).n

Из теоремы Коши и второй теоремы Вейерштрасса следует, что непрерывная на отрезке функция принимает любые значения, заключенные между ее наибольшим и наименьшим значениями на этом отрезке.

Рис. 1.1 иллюстрирует теоремы Коши и Вейерштрасса, а также следствие из них.

На рис. 1.2. в качестве иллюстрации теоремы об обратной функции изображен график непрерывной и строго монотонной на отрезке [a, b] функции f(x), т.е. функции, обладающей свойством: если а £ х₁ < х₂ £ b,то f(x₁) < f(x₂). Обратная функция определяется на отрезке [A, B], где A = f (a), B = f (b), следующим образом: для y, А £ y £ B, полагаем

g(y) = x, если f(x) = y;

свойства непрерывности и строгой монотонности функции f гарантируют существование и единственность такого х, а также строгую монотонность обратной функции g.

Пример 1.5.

Все элементарные функции – х^а, а^х, log_a x, sin x, cos x,arcsin x, arccos x и др. непрерывны в любой точке их области определения; кроме того, в тех точках, где имеют смысл суперпозиции элементарных функций, т.е. функции вида , где f и g-элементарные действительные функции, – они также непрерывны. n

Точка х₀ из области определения функции f(x) называется точкой разрыва этой функции, если функция f(x) не является непрерывной в этой точке. Если при этом существуют оба конечных односторонних предела и , то говорят о точке разрыва I рода; величина называется скачком функции в точке х₀. В любом другом случае говорят о разрыве II рода.

Функция f(x), заданная на некотором промежутке действительной оси, называется кусочно-непрерывной на этом промежутке, если она имеет на нем конечное число точек разрыва I рода.

На рис. 1.3 изображен график функции

Эта функция определена на отрезке [0, 2] и принимает на нем какие угодно большие по величине значения, т.е. не ограничена на нем. Причиной неограниченности является наличие точки разрыва II рода х ₀ = 1, ибо f (1) = 1, а .

В примере 1.3 функция f(x) = sign (x) имеет в точке x = 0 разрыв I рода; величина скачка функции равна 2.