Производная

Рассмотрим действительную функцию y = f(x), определенную в некоторой окрестности точки х0. Обозначим через Dх =х – х0 приращение аргумента, а через Dy =f(х0 + Dх) – f(x0) – приращение функции, соответствующее этому приращению аргумента.

Если существует предел ,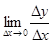

то он называется производной функции f в точке х₀ и обозначается как , .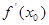

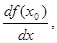
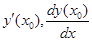Операция вычисления производной называется дифференцированием. Если производная 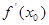– конечна, функция называется дифференцируемой в точке х₀. Функция, дифференцируемая в каждой точке некоторого промежутка, называется дифференцируемой в промежутке.

Дадим геометрическое истолкование производной. В прямоугольной системе координат (см. рис. 1.4) изобразим график функции y = f(x), соответствующийнекоторой окрестности точки х₀. Точка М (х₀, y₀ = f(x₀)) является заданной, а точка N (x, y = f(x)) – произвольной точкой графика. Линия МN – секущая, она образует угол b с осью х, причем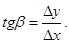

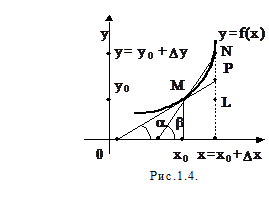Предельное положение секущей при D х ®0 будет соответствовать касательной МР к графику функции f в точке М. Касательная образует с осью х угол a, так что

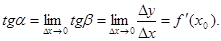
Иными словами, график y = f(x) имеет в точке М = М(x₀ ,,y₀) касательную тогда и только тогда, когда существует производная функции f в точке х₀, причем

tga = f'(x₀).

Дифференцируемая в точке х₀ функция с необходимостью непрерывна в этой точке. Обратное неверно ‑ существуют непрерывные функции, не имеющие производных ни в одной точке своей области определения. n

Приведем таблицу производных элементарных функций:

1) , ;

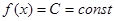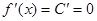2) 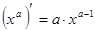, a=const;

3) 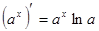, a=const>0, a¹1;

4) 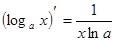; a=const>0, a¹1;

5) ;

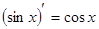6) ;

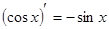7) ;

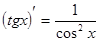8) ;

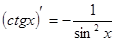9) ;

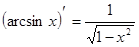10) ;

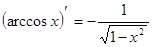11) ;

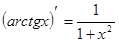12) .

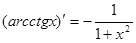Существуют следующие общие правила дифференцирования комбинаций дифференцируемых функций:

1) 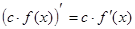, c=const;

2) ;

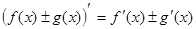3) ;

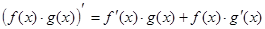4) ;

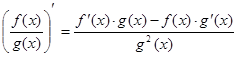5) 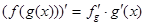, т.е. производная от суперпозиции функций f и g равна произведению их производных по соответствующим аргументам;

6) если y = f(x) и x = g(y) – две взаимно обратные функции и y₀ = f(x₀), то 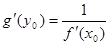n

Если в точке х₀ существует предел для функции y = f(x)

,

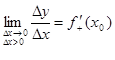то он называется правосторонней производной функции y = f(x) в точке x₀.

На рис. 1.5 в точке М(х₀,y₀) имеем .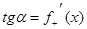

Аналогично определяется левосторонняя производная

.

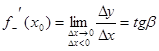Функция f имеет в точке х₀ производную, если значения обеих односторонних производных в этой точке совпадают, причем в этом случае

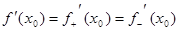.n

Если же 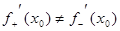, то говорят о наличии в точке М (х₀,y₀) двух полукасательных – правосторонней с углом a и левосторонней с углом b, а сама точка М (х₀,y₀) называется угловой.

Пример 1.6.

Для функции f(x) = abs (x), определяемой как f(x) = x при х ³ 0 и f(x) = -x при х < 0, в 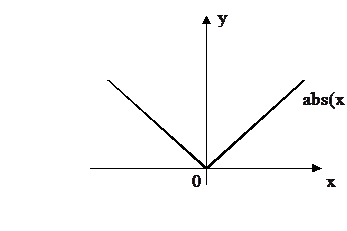точке 0 имеем

, .

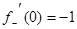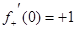Поскольку f_-^'(0) ¹ f₊^'(0), то 0 – угловая точка для функции abs (x).n

Производную f'(x) называют также первой производной или производной первого порядка функции f(x). Рассматривая ее как функцию в некотором интервале значений аргумента х, можно говорить о ее производной, которую называют производной второго порядка или второй производной исходной функции f и обозначают как 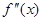и т.д.

Вообще, n-ая производная или производная n-ого порядка определяется индуктивно как

.

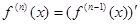Для нее наряду с f ⁽ⁿ⁾(x) используется обозначение 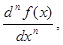n ³ 2.

Производные используют при вычислении пределов функций для раскрытия так называемых неопределенностей. Рассмотрим случай, когда требуется определить 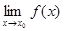, а функция f(x) имеет вид

,

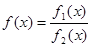причем 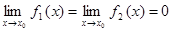, т.е. имеет место неопределенность вида 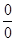. Если функции f₁ и f₂ дифференцируемы, то можно воспользоваться правилом Лопиталя:

.

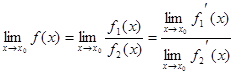Если опять 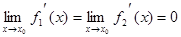и мы снова получаем неопределенность вида 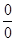, то можно воспользоваться вторыми производными, т.е.

.

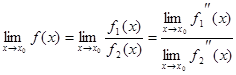Если и здесь получается неопределенность вида 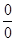, то можно переходить к пределам третьих производных и т.д.

Правило Лопиталя можно применять и для раскрытия неопределенностей вида .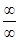

Пример 1.7.

1) Вычислить 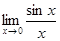. Здесь неопределенность вида 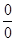. Используем правило Лопиталя.

.

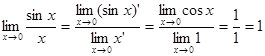2) Вычислить 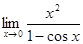. Ясно, что имеем неопределенность вида 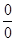. Воспользуемся правилом Лопиталя; это придется сделать дважды.

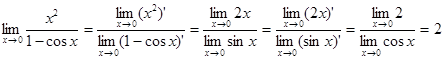n